算法基础（1）之递归、时间空间复杂度

算法基础（1）之递归、时间空间复杂度
参考目录：

递归和栈帧的调用原理

时间复杂度和空间复杂度

斐波那契时间复杂度和空间复杂度分析

我的笔记：

JavaScript之递归

ES6 之函数的扩展尾调用以及尾递归

递归（recursion）

递归是一种很常见的计算编程方法，现在通过阶乘案例来学习递归

demo1:
```
function factorial(num) {
  if(num === 1) return num;
  return num * factorial(num - 1); // 递归求n的阶乘，会递归n次，每次递归内部计算时间是常数，需要保存n个调用记录，复杂度 O(n)
}

const view = factorial(100);
console.time(1);
console.log(view); // 1: 3.568ms
console.timeEnd(1);
```
递归可能会造成栈溢出，在程序执行中，函数通过栈（stack——后进先出）这种数据实现的，每当进入一个函数调用，栈就会增加一层栈帧，每次函数返回，栈就会减少一层栈帧。由于栈的大小不是无限的，所以，递归调用的次数过多，就会导致栈溢出（stack overflow）。

demo2：尾递归
```
// 如果改为尾递归，只需要保留一个调用记录，复杂度为O(1)
function factorial01(n, tntal) {
    if(n === 1) return tntal
    return factorial(n - 1, n * tntal) // 把每一步的乘积传入到递归函数中，每次仅返回递归函数本身，total在函数调用前就会被计算，不会影响函数调用
}
console.time(2)
console.log(factorial01(5, 1)) // 120
console.timeEnd(2) // 2: 0.14404296875ms
```
栈帧

每一个栈帧对应着一个未运行完的函数，栈帧中保存了该函数的返回地址和局部变量。

栈帧也叫过程活动记录，是编译器用来实现过程/函数调用的一种数据结构。从逻辑上讲，栈帧就是一个函数执行的环境：函数参数、函数的局部变量、函数执行完后返回到哪里等。

栈是从高地址向低地址延伸的。每一个函数的每次调用，都有他自己独立的一个栈帧，这个栈帧中维持着所需要的各种信息。寄存器ebp指向当前栈帧的底部（高地址），寄存器esp指向当前的栈帧的顶部（低地址）

注意：
- EBP指向当前位于系统栈最上边的一个栈帧的底部，而不是系统栈的底部。严格说来，“栈帧底部”和“栈底”是不通的概念
- ESP所指的是栈帧顶部和系统的顶部是同一个位置
引入复杂度

递归算法的时间复杂度：递归的总次数*每次递归的数量。

递归算法的空间复杂度：递归的深度*每次递归创建变量的个数。

时间复杂度

算法的时间复杂度是一个函数，它定量描述了该算法的运行时间。这是一个代表算法输入的字符串的长度的函数。时间复杂度通常用大O符号表示，不包括这个函数的低阶项和首项系数。

使用这种方式时，时间复杂度可被成为是渐进的，也考察输入值大小趋近无穷时的情况。

名词解释：
- n：问题的规模，n是不断变化的。
- T(n)：语句频度或称时间频度——算法解决问题所执行语句的次数。
- f(n)：辅助函数，使得T(n)/f(n)的极限为不等于零的常数，那么称f(n)是T(n)的同数量级函数。
- O：大O符号,一种符号,表示渐进于无穷的行为——大O表示只是说有上界但并不是上确界。
例如，如果一个算法对于任何大小为n（必须比

为了计算时间复杂度，通常会估计算法的操作单元数量，每个单元运行的时间都是相同的。因此，总运行时间和算法的操作单元数量最多相差一个常量系数。

计算方法
1. 一般情况下，算法中的基本操作重复执行的次数是问题规模n的摸个函数，用T(n)表示，若有某个辅助函数f(n)，使得当n趋近于无穷大时，T(n)/f(n)的极限为不等于零的常数，则趁f(n)是T(n)的同数量级函数。记作T(n)=O(f(n))，称O(f(n))为算法的渐进时间复杂度，简称时间复杂度。
  
  分析：随着模块n的增大，算法执行时间的增长率和f(n)的增长率成正比，所以f(n)越小，算法的时间复杂度越低，算法的效率越高。
2. 在计算时间复杂度的时候，先找出算法的基础操作，然后根据相应的各语句确定它的执行次数，再找出T(n)的同数量级（他的同数量级有以下：1，
3. 时间复杂度比较简单的计算方法是：看看有几重for循环，只有一重则时间复杂度为O(n) ，二重则为O(n^2)，依此类推，如果有二分则为O(logn)，二分例如快速幂、二分查找，如果一个for循环套一个二分，那么时间复杂度则为O(nlogn)。
简单算法的时间复杂度举例
```
temp = a; a = b; b = temp;
// 上面语句共三条操作，单条操作的频度为1，即使他有成千上万条操作，也只是个较大的书而已，这一类的时间复杂度为O(1)
```
- O(n)的算法是一些线性算法。例如：
```
let sum = 0; // 频度为1
for(let i = 0; i < n; i++) { // 频度为n
    sum++; // 频度为n
}
// 三行的频度加起来为f(n)= i + n + n = 2n + 1,所以时间复杂度为O(n)，这一类算法中操作次数和n成正比线性增长
```
- log2为底n的对数，一个算法如果能在每一个步骤去掉一半数据元素，如二分检索，举个例子：
```
int i = 1;
while(i <= n) {
    i = i * 2;
}
```
上面代码设第三行的频度是f(n),则：2的f(n)次方<=n；f(n)<=
```
let sum = 0; // 频度为1
for(let i = 0; i < n; i++) { // 频度为n
    for(let j = 0; j < n; j++) { // 频度为n的平方
        sum++; // 频度为n的平方
    }
}
```
时间复杂度按n越大算法越复杂来排的话：

　　常数阶O(1)、对数阶O(logn)、线性阶O(n)、线性对数阶O(nlogn)、平方阶O(n²)、立方阶O(n³)、……k次方阶O(n的k次方)、指数阶O(2的n次方)。

在快速排序中，最坏的情况运行时间是

实际情况下如果不是迫不得已不要用时间复杂度为指数的算法，除非n特别小。

空间复杂度

空间复杂度是一个算法在运行过程中临时占用存储空间的大小（问题规模n的函数），记作

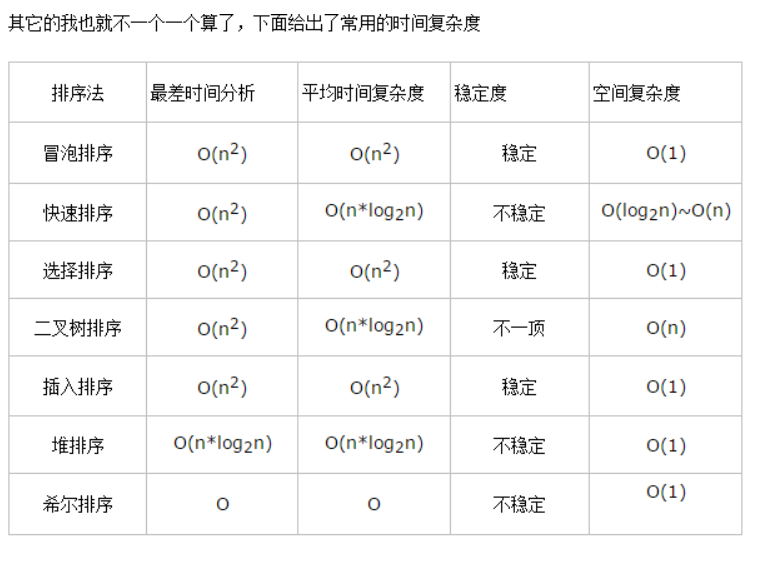
比如直接插入排序的时间复杂度是O(n^2),空间复杂度是O(1) 。

有的算法需要占用的临时工作单元数与解决问题的规模n有关，它随着n的增大而增大，当n较大时，将占用较多的存储单元，例如快速排序和归并排序算法就属于这种情况。

算法的空间复杂度是指算法所需要消耗的空间资源，其计算和表示方法与时间复杂度类似。一般都用复杂度的渐进性来表示。同时间复杂度相比，空间复杂度的分析要简单的多。

插入排序

概念：有一个已经有序的数据序列，要求在这个已经排好的数据序列中插入一个数，但要求插入后此数据序列仍然有序。

可以分为直接插入排序和折半插入排序（二分插入排序）
- 直接插入排序——双重for循环
- 二分插入排序
  - 二分插入排序的基本思想和插入排序一致；都是将某个元素插入到已经有序的序列的正确的位置
  - 和直接插入排序的最大区别是，元素A[i]的位置的方法不一样；直接插入排序是从A[i-1]往前一个个比较，从而找到正确的位置；而二分插入排序，利用前i-1个元素已经是有序的特点结合二分查找的特点，找到正确的位置，从而将A[i]插入，并保持新的序列依旧有序
  - 减少元素之间比较次数，最坏情况o(n^2)，最好情况o(nlogn)：刚好插入位置为二分位置
斐波那契时间复杂度和空间复杂度分析
```
function Fibonacci(n) {
    if(n <= 1) return 1;
    return Fibonacci(n - 1) + Fibonacci(n - 2);
};
console.time(1)
console.log(Fibonacci(20)) // 10946
console.timeEnd(1) // 1: 4.115966796875ms

// console.time(2)
// console.log(Fibonacci(100))
// console.timeEnd(2) // stack overflow 堆栈溢出
```
当n=5时，在递归调用过程中，Fibonacci(3)被计算了2次，Fibonacci(2)被计算了3次，Fibonacci(1)被计算了5次，Fibonacci(0)被计算了3次。

可见递归出口在n>=2是，就会一直在现有函数栈上开辟新的空间，所以容易出现栈溢出。

二叉树的高度为n-1,一个高度为k的二叉树最多可以由

尾递归优化
- 空间复杂度可达到o(1)，但时间复杂度是o(n);
```
function Fibonacci01(n, ac1 = 1, ac2 = 1) {
    if(n <= 1) return ac2
    return Fibonacci01(n - 1, ac2, ac1 + ac2)
}

console.time(3)
console.log(Fibonacci01(100)) // 573147844013817200000
console.timeEnd(3) // 3: 0.52197265625ms
```
相关阅读:
Queue
List
面试1
野指针和空指针
 指针的定义和使用
 多文件编程
 函数声明
 函数样式
 字符串比较
 函数的定义和使用
原文地址：https://www.cnblogs.com/houfee/p/10536763.html

算法基础（1）之递归、时间空间复杂度

递归（recursion）

栈帧

引入复杂度

时间复杂度

空间复杂度

插入排序

斐波那契时间复杂度和空间复杂度分析

尾递归优化