leetcode dp

53. Maximum Subarray

Given an integer array nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.

Example:

Input: [-2,1,-3,4,-1,2,1,-5,4],
Output: 6
Explanation: [4,-1,2,1] has the largest sum = 6.

思路：当前的最大值怎没递归呢？就是取（前一个最大的值）和（前一个值加上当前值）的最大者

dp[i]=max(dp[i-1]+当前值nums[i] ,  之前的最大值max)

class Solution {
  int maxSubArray(vector<int> &nums) {
        int n =nums.size();
        vector<int> dp(n,0);//dp[i] means the maximum subarray ending with nums[i];
        dp[0] = nums[0];
        int max = dp[0];
        
        for(int i = 1; i < n; i++){
            dp[i] = nums[i] + (dp[i - 1] > 0 ? dp[i - 1] : 0); //前面的dp[i-1]小于0则清空重新从0开始计数
            max = max(max, dp[i]); //当前的dp[i]和之前的最大的某个dp比较，取最大
        }
        
        return max;
}
};

64. Minimum Path Sum

Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right which minimizes the sum of all numbers along its path.

Note: You can only move either down or right at any point in time.

Example:

Input:
[
  [1,3,1],
  [1,5,1],
  [4,2,1]
]
Output: 7
Explanation: Because the path 1→3→1→1→1 minimizes the sum.

思路：递归策略：当前的格子等于前一列格子加上一个格子。最左边只能加上一个格子，最上边的只能加做一个格子。

///不优化
class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size(); 
        vector<vector<int> > sum(m, vector<int>(n, grid[0][0]));
        for (int i = 1; i < m; i++)  //左格子
            sum[i][0] = sum[i - 1][0] + grid[i][0];
        for (int j = 1; j < n; j++)  //右格子
            sum[0][j] = sum[0][j - 1] + grid[0][j];
        for (int i = 1; i < m; i++)   //既不是左格子也不是右格子，而是中间的格子
            for (int j = 1; j < n; j++)
                sum[i][j]  = min(sum[i - 1][j], sum[i][j - 1]) + grid[i][j];
        return sum[m - 1][n - 1];  //返回最右下角的格子值
    }
};


////两个一位数组的优化
//思路：当前的格子只和前一个格子和上一个格子有关，所以可以使用两个数组来保存。一个数组pre用来保存前一列的递归值，一个数组cur保存当前列的递归值

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        vector<int> pre(m, grid[0][0]);
        vector<int> cur(m, 0);
        for (int i = 1; i < m; i++)
            pre[i] = pre[i - 1] + grid[i][0];
        for (int j = 1; j < n; j++) { 
            cur[0] = pre[0] + grid[0][j]; 
            for (int i = 1; i < m; i++)
                cur[i] = min(cur[i - 1], pre[i]) + grid[i][j];
            swap(pre, cur); 
        }
        return pre[m - 1];
    }
};


///一个一维数组的优化
//从第二种方法知到，保留的pre数组其实也就是cur数组的前一次，所以可以直接使用一个数组cur就够了

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        vector<int> cur(m, grid[0][0]);
        for (int i = 1; i < m; i++)
            cur[i] = cur[i - 1] + grid[i][0]; 
        for (int j = 1; j < n; j++) {
            cur[0] += grid[0][j]; 
            for (int i = 1; i < m; i++)
                cur[i] = min(cur[i - 1], cur[i]) + grid[i][j];
        }
        return cur[m - 1];
    }
};

第二种方法图解：

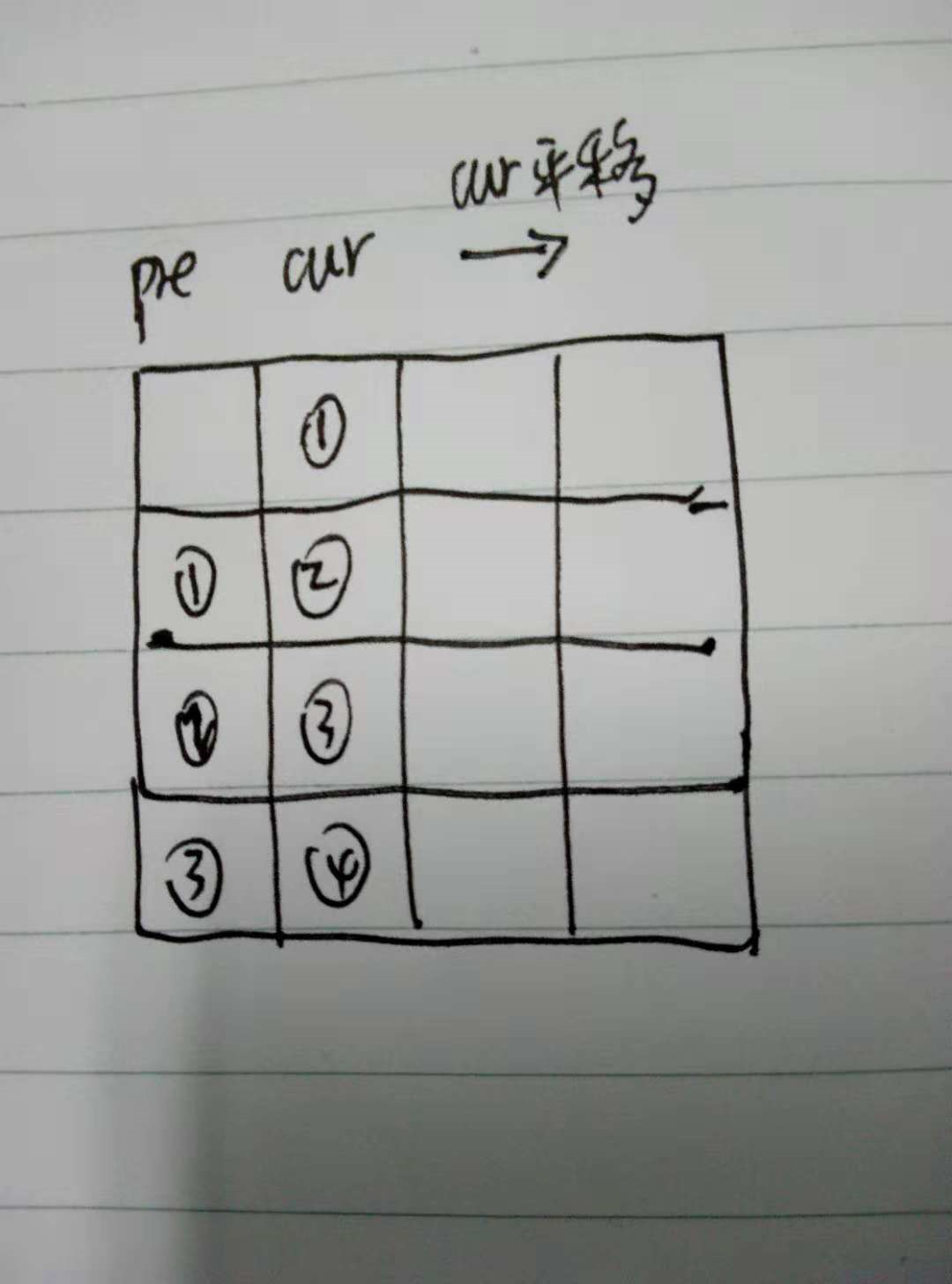
pre代表当前格子的前一个格子，cur代表当前格子+上一个格子+前一个格子，迭代完当前列后，后面的列重复前面的动作。

120. Triangle

Given a triangle, find the minimum path sum from top to bottom. Each step you may move to adjacent numbers on the row below.

For example, given the following triangle

[
     [2],
    [3,4],
   [6,5,7],
  [4,1,8,3]
]

The minimum path sum from top to bottom is 11 (i.e., 2 + 3 + 5 + 1 = 11).

思路：第一时间会想到动态规划，那么自顶向下还是自底向上？自顶向下要保存每次计算的和，所以要消耗一定的空间，而自底向上则简单点，本身的值即为路径和。

int minimumTotal(vector<vector<int> > &triangle) {
    int n = triangle.size();
    vector<int> minlen(triangle.back());
    for (int layer = n-2; layer >= 0; layer--) // 迭代每层
    {
        for (int i = 0; i <= layer; i++) // Check its every 'node'
        {
            // Find the lesser of its two children, and sum the current value in the triangle with it.
            minlen[i] = min(minlen[i], minlen[i+1]) + triangle[layer][i]; 
        }
    }
    return minlen[0];
}

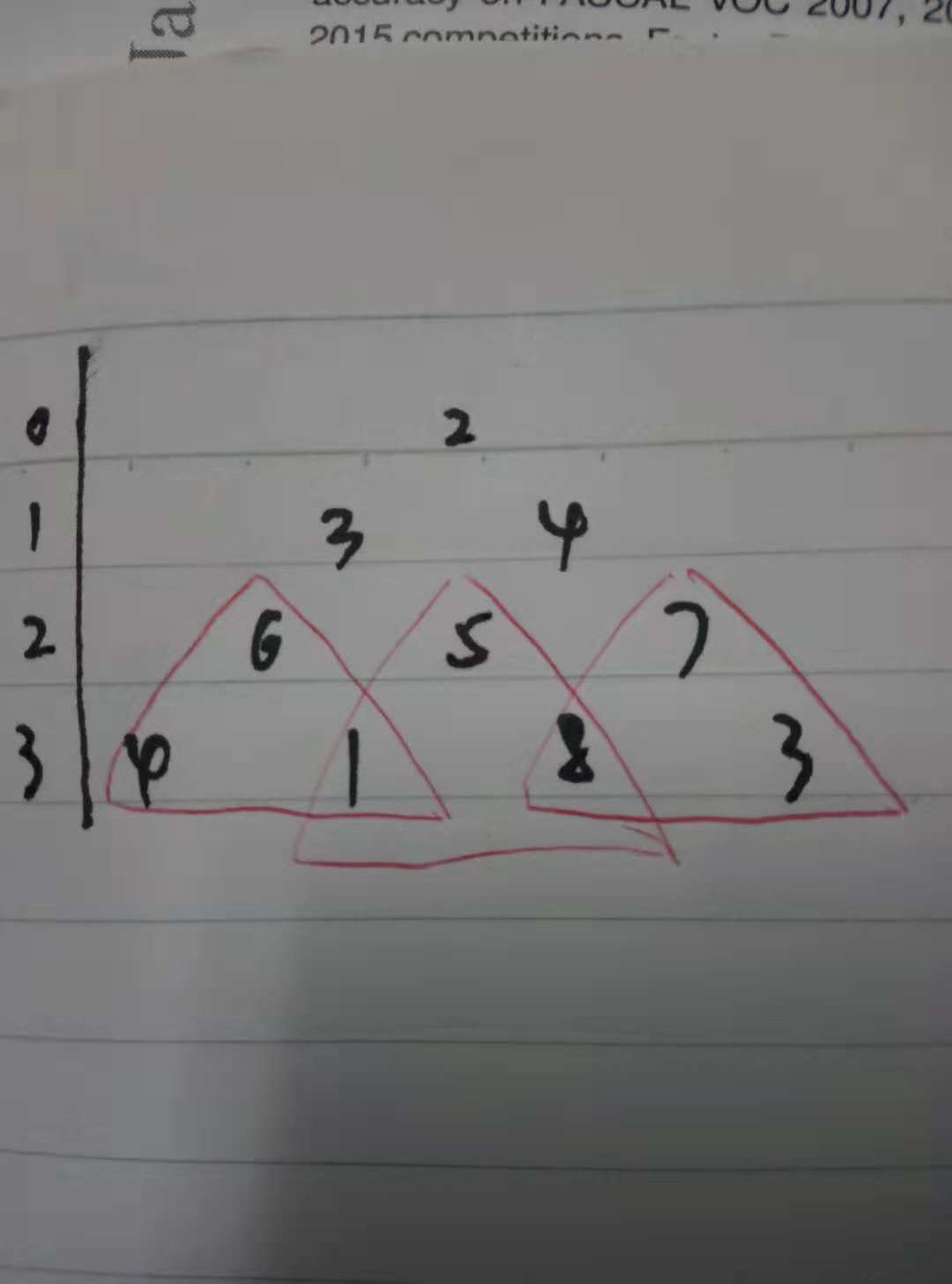
对照上图其实就是先从底下开始，当n=4时，外循环此时是第三层（index=2），然后在内循环里面遍历当前层对应的子节点，如4和1取最小6，保存为minlen[]数组供下一次迭代。