本文总结ML面试常见的问题集
转载来源:https://blog.csdn.net/v_july_v/article/details/78121924
81、已知一组数据的协方差矩阵P,下面关于主分量说法错误的是()
A、主分量分析的最佳准则是对一组数据进行按一组正交基分解, 在只取相同数量分量的条件下,以均方误差计算截尾误差最小
B、在经主分量分解后,协方差矩阵成为对角矩阵
C、主分量分析就是K-L变换
D、主分量是通过求协方差矩阵的特征值得到
正确答案: C
@BlackEyes_SGC:K-L变换与PCA变换是不同的概念,PCA的变换矩阵是协方差矩阵,K-L变换的变换矩阵可以有很多种(二阶矩阵、协方差矩阵、总类内离散度矩阵等等)。当K-L变换矩阵为协方差矩阵时,等同于PCA。
82、关于logit 回归和SVM 不正确的是(A)
A. Logit回归本质上是一种根据样本对权值进行极大似然估计的方法,而后验概率正比于先验概率和似然函数的乘积。logit仅仅是最大化似然函数,并没有最大化后验概率,更谈不上最小化后验概率。A错误
B. Logit回归的输出就是样本属于正类别的几率,可以计算出概率,正确
C. SVM的目标是找到使得训练数据尽可能分开且分类间隔最大的超平面,应该属于结构风险最小化。
D. SVM可以通过正则化系数控制模型的复杂度,避免过拟合。
@BlackEyes_SGC:Logit回归目标函数是最小化后验概率,Logit回归可以用于预测事件发生概率的大小,SVM目标是结构风险最小化,SVM可以有效避免模型过拟合。
A、主分量分析的最佳准则是对一组数据进行按一组正交基分解, 在只取相同数量分量的条件下,以均方误差计算截尾误差最小
B、在经主分量分解后,协方差矩阵成为对角矩阵
C、主分量分析就是K-L变换
D、主分量是通过求协方差矩阵的特征值得到
正确答案: C
@BlackEyes_SGC:K-L变换与PCA变换是不同的概念,PCA的变换矩阵是协方差矩阵,K-L变换的变换矩阵可以有很多种(二阶矩阵、协方差矩阵、总类内离散度矩阵等等)。当K-L变换矩阵为协方差矩阵时,等同于PCA。
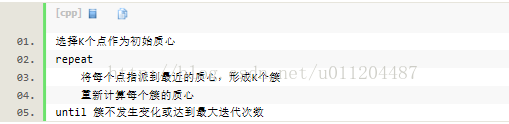
kmeans的复杂度?
时间复杂度:O(tKmn),其中,t为迭代次数,K为簇的数目,m为记录数,n为维数空间复杂度:O((m+K)n),其中,K为簇的数目,m为记录数,n为维数

时间复杂度:O(tKmn),其中,t为迭代次数,K为簇的数目,m为记录数,n为维数空间复杂度:O((m+K)n),其中,K为簇的数目,m为记录数,n为维数
A. Logit回归本质上是一种根据样本对权值进行极大似然估计的方法,而后验概率正比于先验概率和似然函数的乘积。logit仅仅是最大化似然函数,并没有最大化后验概率,更谈不上最小化后验概率。A错误
B. Logit回归的输出就是样本属于正类别的几率,可以计算出概率,正确
C. SVM的目标是找到使得训练数据尽可能分开且分类间隔最大的超平面,应该属于结构风险最小化。
D. SVM可以通过正则化系数控制模型的复杂度,避免过拟合。
@BlackEyes_SGC:Logit回归目标函数是最小化后验概率,Logit回归可以用于预测事件发生概率的大小,SVM目标是结构风险最小化,SVM可以有效避免模型过拟合。
83、输入图片大小为200×200,依次经过一层卷积(kernel size 5×5,padding 1,stride 2),pooling(kernel size 3×3,padding 0,stride 1),又一层卷积(kernel size 3×3,padding 1,stride 1)之后,输出特征图大小为()
A 95
B 96
C 97
D 98
E 99
F 100
正确答案:C
@BlackEyes_SGC:计算尺寸不被整除只在GoogLeNet中遇到过。卷积向下取整,池化向上取整。
本题 (200-5+2*1)/2+1 为99.5,取99
(99-3)/1+1 为97
(97-3+2*1)/1+1 为97
研究过网络的话看到stride为1的时候,当kernel为 3 padding为1或者kernel为5 padding为2 一看就是卷积前后尺寸不变。
计算GoogLeNet全过程的尺寸也一样。
A 95
B 96
C 97
D 98
E 99
F 100
正确答案:C
@BlackEyes_SGC:计算尺寸不被整除只在GoogLeNet中遇到过。卷积向下取整,池化向上取整。
本题 (200-5+2*1)/2+1 为99.5,取99
(99-3)/1+1 为97
(97-3+2*1)/1+1 为97
研究过网络的话看到stride为1的时候,当kernel为 3 padding为1或者kernel为5 padding为2 一看就是卷积前后尺寸不变。
计算GoogLeNet全过程的尺寸也一样。
84 影响聚类算法结果的主要因素有(B、C、D )
A.已知类别的样本质量;
B.分类准则;
C.特征选取;
D.模式相似性测度
A.已知类别的样本质量;
B.分类准则;
C.特征选取;
D.模式相似性测度
85 模式识别中,马式距离较之于欧式距离的优点是(C、D)
A.平移不变性;
B.旋转不变性;
C尺度不变性;
D.考虑了模式的分布
A.平移不变性;
B.旋转不变性;
C尺度不变性;
D.考虑了模式的分布
欧氏距离(Euclidean distance)也称欧几里得度量、欧几里得度量,是一个通常采用的距离定义,它是在m维空间中两个点之间的真实距离。在二维和三维空间中的欧氏距离的就是两点之间的距离。
缺点:就大部分统计问题而言,欧氏距离是不能令人满意的。(每个坐标对欧氏距离的贡献是同等的。当坐标表示测量值时,它们往往带有大小不等的随机波动,在这种情况下,合理的方法是对坐标加权,使变化较大的坐标比变化较小的坐标有较小的权系数,这就产生了各种距离。当各个分量为不同性质的量时,“距离”的大小与指标的单位有关。它将样品的不同属性(即各指标或各变量)之间的差别等同看待,这一点有时不能满足实际要求。没有考虑到总体变异对距离远近的影响。
马氏距离(Mahalanobis distance)是由印度统计学家马哈拉诺比斯提出的,表示数据的协方差距离。为两个服从同一分布并且其协方差矩阵为Σ的随机变量与的差异程度:如果协方差矩阵为单位矩阵,那么马氏距离就简化为欧氏距离,如果协方差矩阵为对角阵,则其也可称为正规化的欧氏距离。它是一种有效的计算两个未知样本集的相似度的方法。对于一个均值为μ,协方差矩阵为Σ的多变量向量,样本与总体的马氏距离为(dm)^2=(x-μ)'Σ^(-1)(x-μ)。 在绝大多数情况下,马氏距离是可以顺利计算的,但是马氏距离的计算是不稳定的,不稳定的来源是协方差矩阵,这也是马氏距离与欧式距离的最大差异之处。

优点:它不受量纲的影响,两点之间的马氏距离与原始数据的测量单位无关。(它考虑到各种特性之间的联系(例如:一条关于身高的信息会带来一条关于体重的信息,因为两者是有关联的)并且是尺度无关的(scale-invariant),即独立于测量尺度);由标准化数据和中心化数据(即原始数据与均值之差)计算出的二点之间的马氏距离相同。马氏距离还可以排除变量之间的相关性的干扰。
缺点:夸大了变化微小的变量的作用。受协方差矩阵不稳定的影响,马氏距离并不总是能顺利计算出。
86 影响基本K-均值算法的主要因素有(BD)
A.样本输入顺序;
B.模式相似性测度;
C.聚类准则;
D.初始类中心的选取
A.样本输入顺序;
B.模式相似性测度;
C.聚类准则;
D.初始类中心的选取
87 在统计模式分类问题中,当先验概率未知时,可以使用(BD)
A. 最小损失准则;
B. 最小最大损失准则;
C. 最小误判概率准则;
D. N-P判决
A. 最小损失准则;
B. 最小最大损失准则;
C. 最小误判概率准则;
D. N-P判决
在贝叶斯决策中,对于先验概率p(y),分为已知和未知两种情况。
1. p(y)已知,直接使用贝叶斯公式求后验概率即可;
2. p(y)未知,可以使用聂曼-皮尔逊决策(N-P决策)来计算决策面。
而最大最小损失规则主要就是使用解决最小损失规则时先验概率未知或难以计算的问题的。
88 如果以特征向量的相关系数作为模式相似性测度,则影响聚类算法结果的主要因素有(BC)
A. 已知类别样本质量;
B. 分类准则;
C. 特征选取;
D. 量纲欧式距离具有(A B );
A. 已知类别样本质量;
B. 分类准则;
C. 特征选取;
D. 量纲欧式距离具有(A B );
89 马式距离具有(A B C D )
A. 平移不变性;
B. 旋转不变性;
C. 尺度缩放不变性;
D. 不受量纲影响的特性
A. 平移不变性;
B. 旋转不变性;
C. 尺度缩放不变性;
D. 不受量纲影响的特性
90 你有哪些deep learning(rnn、cnn)调参的经验?
@萧瑟,来源:https://www.zhihu.com/question/41631631/answer/94816420
参数初始化
下面几种方式,随便选一个,结果基本都差不多。但是一定要做。否则可能会减慢收敛速度,影响收敛结果,甚至造成Nan等一系列问题。
下面的n_in为网络的输入大小,n_out为网络的输出大小,n为n_in或(n_in+n_out)*0.5
Xavier初始法论文:http://jmlr.org/proceedings/papers/v9/glorot10a/glorot10a.pdf
He初始化论文:https://arxiv.org/abs/1502.01852
- uniform均匀分布初始化:w = np.random.uniform(low=-scale, high=scale, size=[n_in,n_out])
- Xavier初始法,适用于普通激活函数(tanh,sigmoid):scale = np.sqrt(3/n)
- He初始化,适用于ReLU:scale = np.sqrt(6/n)
- normal高斯分布初始化:w = np.random.randn(n_in,n_out) * stdev # stdev为高斯分布的标准差,均值设为0
- Xavier初始法,适用于普通激活函数 (tanh,sigmoid):stdev = np.sqrt(n)
- He初始化,适用于ReLU:stdev = np.sqrt(2/n)
- svd初始化:对RNN有比较好的效果。参考论文:https://arxiv.org/abs/1312.6120
数据预处理方式
- zero-center ,这个挺常用的.X -= np.mean(X, axis = 0) # zero-centerX /= np.std(X, axis = 0) # normalize
- PCA whitening,这个用的比较少.
训练技巧
- 要做梯度归一化,即算出来的梯度除以minibatch size
- clip c(梯度裁剪): 限制最大梯度,其实是value = sqrt(w1^2+w2^2….),如果value超过了阈值,就算一个衰减系系数,让value的值等于阈值: 5,10,15
- dropout对小数据防止过拟合有很好的效果,值一般设为0.5,小数据上dropout+sgd在我的大部分实验中,效果提升都非常明显.因此可能的话,建议一定要尝试一下。 dropout的位置比较有讲究, 对于RNN,建议放到输入->RNN与RNN->输出的位置.关于RNN如何用dropout,可以参考这篇论文:http://arxiv.org/abs/1409.2329
- adam,adadelta等,在小数据上,我这里实验的效果不如sgd, sgd收敛速度会慢一些,但是最终收敛后的结果,一般都比较好。如果使用sgd的话,可以选择从1.0或者0.1的学习率开始,隔一段时间,在验证集上检查一下,如果cost没有下降,就对学习率减半. 我看过很多论文都这么搞,我自己实验的结果也很好. 当然,也可以先用ada系列先跑,最后快收敛的时候,更换成sgd继续训练.同样也会有提升.据说adadelta一般在分类问题上效果比较好,adam在生成问题上效果比较好。
- 除了gate之类的地方,需要把输出限制成0-1之外,尽量不要用sigmoid,可以用tanh或者relu之类的激活函数.1. sigmoid函数在-4到4的区间里,才有较大的梯度。之外的区间,梯度接近0,很容易造成梯度消失问题。2. 输入0均值,sigmoid函数的输出不是0均值的。
- rnn的dim和embdding size,一般从128上下开始调整. batch size,一般从128左右开始调整.batch size合适最重要,并不是越大越好.
- word2vec初始化,在小数据上,不仅可以有效提高收敛速度,也可以可以提高结果.
- 尽量对数据做shuffle
- LSTM 的forget gate的bias,用1.0或者更大的值做初始化,可以取得更好的结果,来自这篇论文:http://jmlr.org/proceedings/papers/v37/jozefowicz15.pdf, 我这里实验设成1.0,可以提高收敛速度.实际使用中,不同的任务,可能需要尝试不同的值.
- Batch Normalization据说可以提升效果,不过我没有尝试过,建议作为最后提升模型的手段,参考论文:Accelerating Deep Network Training by Reducing Internal Covariate Shift
- 如果你的模型包含全连接层(MLP),并且输入和输出大小一样,可以考虑将MLP替换成Highway Network,我尝试对结果有一点提升,建议作为最后提升模型的手段,原理很简单,就是给输出加了一个gate来控制信息的流动,详细介绍请参考论文: http://arxiv.org/abs/1505.00387
- 来自@张馨宇的技巧:一轮加正则,一轮不加正则,反复进行。
Ensemble
Ensemble是论文刷结果的终极核武器,深度学习中一般有以下几种方式
- 同样的参数,不同的初始化方式
- 不同的参数,通过cross-validation,选取最好的几组
- 同样的参数,模型训练的不同阶段,即不同迭代次数的模型。
- 不同的模型,进行线性融合. 例如RNN和传统模型.
更多深度学习技巧,请参见专栏:炼丹实验室 - 知乎专栏