序言:
对于小目标图像分割任务,一副图画中往往只有一两个目标,这样会加大网络训练难度,一般有三种方法解决:
1、选择合适的loss,对网络进行合理优化,关注较小的目标。
2、改变网络结构,使用attention机制。
3、类属attention机制,即先检测目标区域,裁剪后再分割训练。
场景:
现在以U-net网络为基础,使用keras进行实现小目标的分割。
Loss函数:
1、Log loss
对于二分类任务,log loss如下:
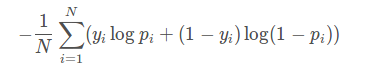
其中,yi为输入实例xixi的真实类别, pi为预测输入实例 xi属于类别 1 的概率。对所有样本的对数损失表示对每个样本的对数损失的平均值。
这个loss函数每一次梯度的回传对每一个类别具有相同的关注度,所以容易受到类别不平衡的影响。
这种情况参照airbus-ship-detection。这个任务是检测海面上的船只,整个图片中大海占幅较大,所以采用一些技巧:使用montage拼接图片,对只有大海的图片进行采样来减少图片大小。
2、WCE loss(weighted cross-entropy)
带权重的交叉熵
二分类WCE:
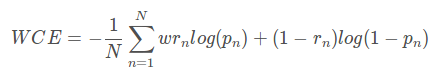
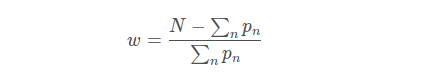
这个loss的缺点时需要人为的调整困难样本的权重,增加调整难度。
3、Focal loss
能否使网络主动学习困难样本呢?
focal loss的提出是在目标检测领域,为了解决正负样本比例严重失调的问题。
focal函数公式:
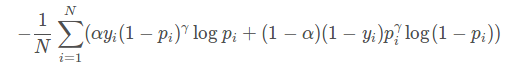
对比上面其实就是多了 (1-pi)r 。
loss值随样本概率变大而变小。
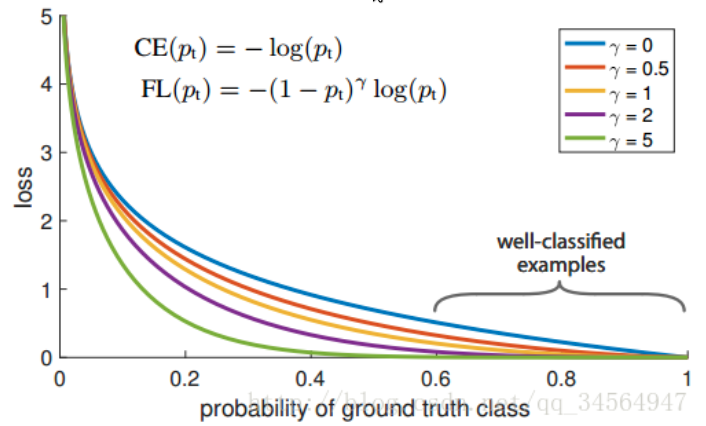
基本思想是,对于类别极度不平衡的情况下,网络如果在log loss下会倾向只预测负样本,并且负样本的预测概率会非常高,回传的梯度也很大。
但是如果添加了上述项,则focal 函数会使预测概率大的样本的loss变小,而预测概率小的样本的loss变大,从而加强了对正样本的关注度。
from keras import backend as K ''' Compatible with tensorflow backend ''' def focal_loss(gamma=2., alpha=.25): def focal_loss_fixed(y_true, y_pred): pt_1 = tf.where(tf.equal(y_true, 1), y_pred, tf.ones_like(y_pred)) pt_0 = tf.where(tf.equal(y_true, 0), y_pred, tf.zeros_like(y_pred)) return -K.sum(alpha * K.pow(1. - pt_1, gamma) * K.log(pt_1))-K.sum((1-alpha) * K.pow( pt_0, gamma) * K.log(1. - pt_0)) return focal_loss_fixed
model_prn.compile(optimizer=optimizer, loss=[focal_loss(alpha=.25, gamma=2)])
使用U-net输入输出都是一张图,直接使用会导致loss值很大。而且调参alpha和gamma也麻烦。
4、Dice loss
直观理解为两个轮廓的相似程度。
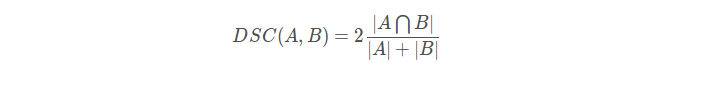
或则表示为:
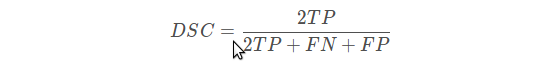
二分类的dice loss:
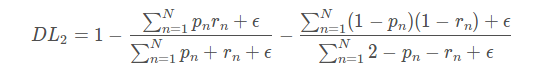
def dice_coef(y_true, y_pred, smooth=1): intersection = K.sum(y_true * y_pred, axis=[1,2,3]) union = K.sum(y_true, axis=[1,2,3]) + K.sum(y_pred, axis=[1,2,3]) return K.mean( (2. * intersection + smooth) / (union + smooth), axis=0) def dice_coef_loss(y_true, y_pred): 1 - dice_coef(y_true, y_pred, smooth=1)
使用dice loss有时会不可信,原因是对于sofemax或log loss其梯度简言之是p-t ,t为目标值,p为预测值。而dice loss 为 2t2 / (p+t)2
如果p,t过小会导致梯度变化剧烈,导致训练困难。
5、IOU loss
类比dice loss,IOU函数公式:
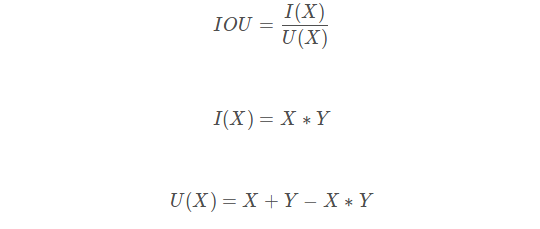
def IoU(y_true, y_pred, eps=1e-6): if np.max(y_true) == 0.0: return IoU(1-y_true, 1-y_pred) ## empty image; calc IoU of zeros intersection = K.sum(y_true * y_pred, axis=[1,2,3]) union = K.sum(y_true, axis=[1,2,3]) + K.sum(y_pred, axis=[1,2,3]) - intersection return -K.mean( (intersection + eps) / (union + eps), axis=0)
IOU loss的缺点呢同DICE loss是相类似的,训练曲线可能并不可信,训练的过程也可能并不稳定,有时不如使用softmax loss等的曲线有直观性,通常而言softmax loss得到的loss下降曲线较为平滑。
6、Tversky loss
Tversky loss使dice系数和jaccard系数的一种广义系数。
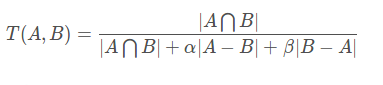
观察可得当设置α=β=0.5,此时Tversky系数就是Dice系数。
而当设置α=β=1时,此时Tversky系数就是Jaccard系数。
∣A−B∣则意味着是FP(假阳性),而∣B−A∣则意味着是FN(假阴性);α和β分别控制假阴性和假阳性。通过调整α和β我们可以控制假阳性和假阴性之间的权衡。
def tversky(y_true, y_pred): y_true_pos = K.flatten(y_true) y_pred_pos = K.flatten(y_pred) true_pos = K.sum(y_true_pos * y_pred_pos) false_neg = K.sum(y_true_pos * (1-y_pred_pos)) false_pos = K.sum((1-y_true_pos)*y_pred_pos) alpha = 0.7 return (true_pos + smooth)/(true_pos + alpha*false_neg + (1-alpha)*false_pos + smooth) def tversky_loss(y_true, y_pred): return 1 - tversky(y_true,y_pred) def focal_tversky(y_true,y_pred): pt_1 = tversky(y_true, y_pred) gamma = 0.75 return K.pow((1-pt_1), gamma)
7、敏感性-特异性loss
首先敏感性就是召回率,检测出确实有病的能力:
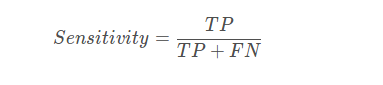
特异性,检测出确实没病的能力:
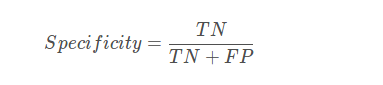
综合
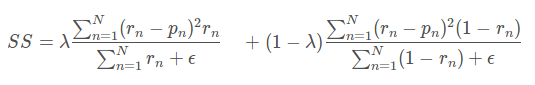
其中左边为病灶像素的错误率即,1−Sensitivity,而不是正确率,所以设置λ 为0.05。其中(rn−pn)2是为了得到平滑的梯度。
8、Generalized dice loss
在使用DICE loss时,对小目标是十分不利的,因为在只有前景和背景的情况下,小目标一旦有部分像素预测错误,那么就会导致Dice大幅度的变动,从而导致梯度变化剧烈,训练不稳定。
当病灶分割有多个区域时,一般针对每一类都会有一个DICE,而Generalized Dice index将多个类别的dice进行整合,使用一个指标对分割结果进行量化。
GDL公式:
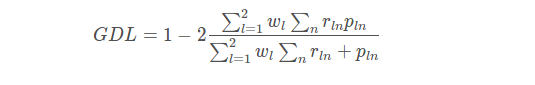
其中rln为类别l在第n个像素的标准值(GT),而pln为相应的预测概率值。此处最关键的是wl,为每个类别的权重。其中
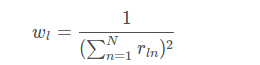
这样,GDL就能平衡病灶区域和Dice系数之间的平衡。
def generalized_dice_coeff(y_true, y_pred): Ncl = y_pred.shape[-1] w = K.zeros(shape=(Ncl,)) w = K.sum(y_true, axis=(0,1,2)) w = 1/(w**2+0.000001) # Compute gen dice coef: numerator = y_true*y_pred numerator = w*K.sum(numerator,(0,1,2,3)) numerator = K.sum(numerator) denominator = y_true+y_pred denominator = w*K.sum(denominator,(0,1,2,3)) denominator = K.sum(denominator) gen_dice_coef = 2*numerator/denominator return gen_dice_coef def generalized_dice_loss(y_true, y_pred): return 1 - generalized_dice_coeff(y_true, y_pred)
以上本质上都是根据评测标准设计的loss function,有时候普遍会受到目标太小的影响,导致训练的不稳定;对比可知,直接使用log loss等的loss曲线一般都是相比较光滑的。
9、BCE + dice loss(BCE : Binary Cross Entropy)
说白了,添加二分类交叉熵损失函数。在数据较为平衡的情况下有改善作用,但是在数据极度不均衡的情况下,交叉熵损失会在几个训练之后远小于Dice 损失,效果会损失。
import keras.backend as K from keras.losses import binary_crossentropy def dice_coef(y_true, y_pred, smooth=1): intersection = K.sum(y_true * y_pred, axis=[1,2,3]) union = K.sum(y_true, axis=[1,2,3]) + K.sum(y_pred, axis=[1,2,3]) return K.mean( (2. * intersection + smooth) / (union + smooth), axis=0) def dice_p_bce(in_gt, in_pred): return 1e-3*binary_crossentropy(in_gt, in_pred) - dice_coef(in_gt, in_pred)