(n+1)个控制点可以定义一条n次贝塞尔曲线
如下图,P1、P2、P3三个点可以定义一条二次贝塞尔曲线。
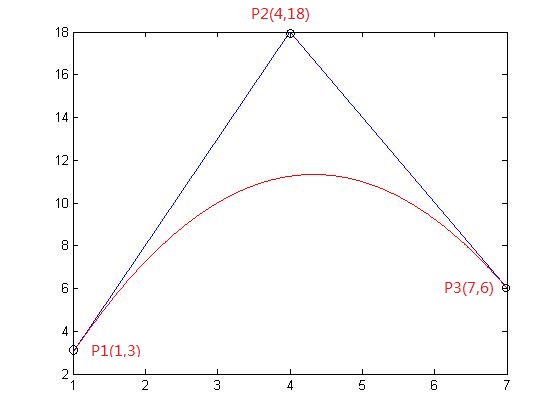
对于贝塞尔曲线的原理,我们先不去解释,先说明如何应用。
常见的应用是:给出一系列的控制点,要求拟合出一条贝塞尔曲线。
==============================================================================================
先给出公式
一阶贝塞尔曲线(也就是直线)参数方程:

二阶贝塞尔曲线参数方程:
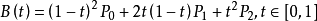
三阶贝塞尔曲线参数方程:
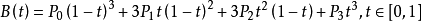
一般参数:
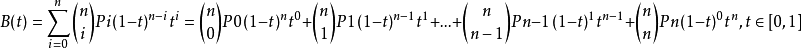
===============================================================================================
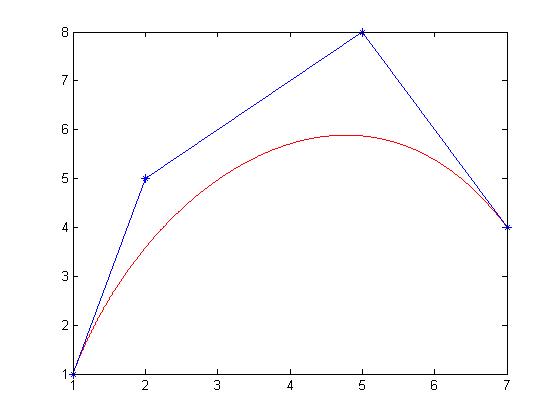
算例1:已知四个控制点P0(1,1)、P1(2,5)、P2(5,8)、P3(7,4),构造一条三阶贝塞尔曲线。
将这四个点带入上面的三阶贝塞尔参数方程中:
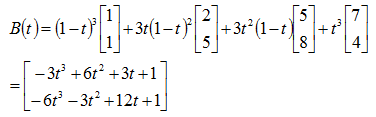
所以得到:
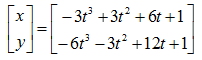
下面在matlab中执行:
%绘制特征多边形
x=[1,2,5,7];
y=[1,5,8,4];
plot(x,y,'-*');
hold on;
%绘制贝塞尔曲线
t=0:0.001:1;
x=1-3*power(t,3)+6*power(t,2)+3*t;
y=1-6*power(t,3)-3*power(t,2)+12*t;
plot(x,y,'r');
结果如下图: