Vanya decided to walk in the field of size n × n cells. The field contains m apple trees, the i-th apple tree is at the cell with coordinates (xi, yi). Vanya moves towards vector (dx, dy). That means that if Vanya is now at the cell (x, y), then in a second he will be at cell 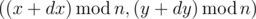 . The following condition is satisfied for the vector:
. The following condition is satisfied for the vector: 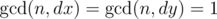 , where
, where 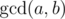 is the largest integer that divides both a and b. Vanya ends his path when he reaches the square he has already visited.
is the largest integer that divides both a and b. Vanya ends his path when he reaches the square he has already visited.
Vanya wonders, from what square of the field he should start his path to see as many apple trees as possible.
The first line contains integers n, m, dx, dy(1 ≤ n ≤ 106, 1 ≤ m ≤ 105, 1 ≤ dx, dy ≤ n) — the size of the field, the number of apple trees and the vector of Vanya's movement. Next m lines contain integers xi, yi (0 ≤ xi, yi ≤ n - 1) — the coordinates of apples. One cell may contain multiple apple trees.
Print two space-separated numbers — the coordinates of the cell from which you should start your path. If there are several answers you are allowed to print any of them.
In the first sample Vanya's path will look like: (1, 3) - (3, 1) - (0, 4) - (2, 2) - (4, 0) - (1, 3)
In the second sample: (0, 0) - (1, 1) - (0, 0)
【分析】
这道题目相对比较简单了。
题意:在一个n * n的棋盘上,有m棵给定坐标的苹果树,选定一个起点(x, y),每次以横坐标+dx(mod n),纵坐标 +dy(mod n)的形式进行移动,其中gcd(dx, n) = gcd(dy, n) = 1,询问选择哪个起点能经过最多的苹果树?
因为有gcd(dx, n) = gcd(dy, n) = 1 所以可以得知行走的路线一定是一个循环,并且循环的长度为n,且能够经过每一个x坐标和每一个y坐标。
我们不妨将起点设在x为0的位置,然后预处理出到其他的x坐标所需要变化的y值,然后就可以将苹果树进行"平移"到x坐标为0上,然后就可以做了。