Vasya is studying in the last class of school and soon he will take exams. He decided to study polynomials. Polynomial is a function P(x) = a0 + a1x1 + ... + anxn. Numbers ai are called coefficients of a polynomial, non-negative integer n is called adegree of a polynomial.
Vasya has made a bet with his friends that he can solve any problem with polynomials. They suggested him the problem: "Determine how many polynomials P(x) exist with integer non-negative coefficients so that 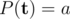 , and
, and  , where
, where  and b are given positive integers"?
and b are given positive integers"?
Vasya does not like losing bets, but he has no idea how to solve this task, so please help him to solve the problem.
The input contains three integer positive numbers  no greater than 1018.
no greater than 1018.
If there is an infinite number of such polynomials, then print "inf" without quotes, otherwise print the reminder of an answer modulo 109 + 7.
|
1
|
1
|
【分析】
题意:给出三个正整数t,a,b。
问有多少个形如P(x) = a0 + a1 * x + a2 * (x ^ 2) + ....+an * (x ^ n) {ai >= 0 | 0<= i <=n} 的多项式满足P(t) = a,且P(a) = b。注意n未给出。
有意思的一道题。
答案只有三种情况:
1、t = a = b = 1,Ans = INF。显然,n可以取到任意大。
2、t = a = b > 1,Ans = 2。也比较显然,既P(t) = t,仅在 n = 0, a0 = t和 n = 1, a1 = 1, a0 = 0的时候成立,n再大 $t^n$ 就会导致答案大于t了。
3、其他情况下最多一组解。
证明:
首先由P(t) = a 易知 多项式sum{ai | 0<= i <=n} <= a,且仅在t = 1的时候取等号。
①t > 1
假设存在一个多项式P(a) = a0 + a1 * a + a2 * (a ^ 2) +.... +an * (a ^ n) = b,我们尝试将其中任意一项 (a ^ k)的系数 ak 减 1 (k >= 1 且 ak > 0)。
整体的值减少了(a ^ k), 将a ^ k 化为 (a ^ k1) * (a ^ k2),(k1+k2 = k 且 k1 <= k2),把a ^ k1当做系数,将会使整个多项式的系数大于等于a(系数增加了至少a - 1),因此不满足条件。
所以可知,如果存在一个多项式P(a)满足条件,一定不存在其他的多项式满足条件,即最多只存在一个多项式符合条件。
想要得到这个多项式也很简单,即相当于对b进行进制转换,变成a进制,然后再将t带入验证即可。
②t = 1
P(1) = a0 + a1 + a2 + .. an = a,P(a) = a0 + a1 * a + a2 * (a ^ 2) + .. an * (a ^ n) = b;
看到系数和已经被确定了为a了,接下来证明跟上面一样的...
代码没写....