【JZOJ3423】Vani和Cl2捉迷藏&【BZOJ1143】祭祀river

description

vani和cl2在一片树林里捉迷藏……

这片树林里有N座房子，M条有向道路，组成了一张有向无环图。

树林里的树非常茂密，足以遮挡视线，但是沿着道路望去，却是视野开阔。如果从房子A沿着路走下去能够到达B，那么在A和B里的人是能够相互望见的。

现在cl2要在这N座房子里选择K座作为藏身点，同时vani也专挑cl2作为藏身点的房子进去寻找，为了避免被vani看见，cl2要求这K个藏身点的任意两个之间都没有路径相连。

为了让vani更难找到自己，cl2想知道最多能选出多少个藏身点？

---

在遥远的东方，有一个神秘的民族，自称Y族。他们世代居住在水面上，奉龙王为神。每逢重大庆典， Y族都
会在水面上举办盛大的祭祀活动。我们可以把Y族居住地水系看成一个由岔口和河道组成的网络。每条河道连接着
两个岔口，并且水在河道内按照一个固定的方向流动。显然，水系中不会有环流（下图描述一个环流的例子）。

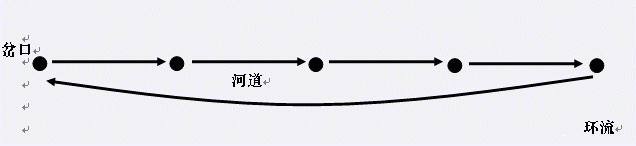
　　由于人数众多的原因，Y族的祭祀活动会在多个岔口上同时举行。出于对龙王的尊重，这些祭祀地点的选择必
须非常慎重。准确地说，Y族人认为，如果水流可以从一个祭祀点流到另外一个祭祀点，那么祭祀就会失去它神圣
的意义。族长希望在保持祭祀神圣性的基础上，选择尽可能多的祭祀的地点。

---

analysis

• 考场想了个(naive)的伪正解

• (O(n^2))处理出两两点是否可达，然后相当于求一个最大完全图，其中两两点互不可达

• 不就求一个最大团，但是(T90)，怎么搞都过不了

• 正解先用(floyd)搞一个什么傻逼传递闭包（对就是预处理两两点是否可达）

• 因为最小路径覆盖数(=n-)二分图最大匹配数，于是拆点然后跑一个匈牙利就行

• 大概就这样吧

---

code

#pragma GCC optimize("O3")
#pragma G++ optimize("O3")
#include<stdio.h>
#include<string.h>
#include<algorithm>
#define MAXN 205
#define ll long long
#define reg register ll
#define fo(i,a,b) for (reg i=a;i<=b;++i)
#define fd(i,a,b) for (reg i=a;i>=b;--i)

using namespace std;

bool bz[MAXN][MAXN];
bool flag[MAXN];
ll a[MAXN][MAXN];
ll f[MAXN];
ll n,m,ans;

inline ll read()
{
	ll x=0,f=1;char ch=getchar();
	while (ch<'0' || '9'<ch){if (ch=='-')f=-1;ch=getchar();}
	while ('0'<=ch && ch<='9')x=x*10+ch-'0',ch=getchar();
	return x*f;
}
inline bool find(ll x)
{
	fo(i,1,a[x][0])if (flag[a[x][i]])
	{
		flag[a[x][i]]=0;
		if (!f[a[x][i]] || find(f[a[x][i]])){f[a[x][i]]=x;return 1;}
	}
	return 0;
}
int main()
{
	freopen("T2.in","r",stdin);
	n=read(),m=read();
	fo(i,1,m)bz[read()][read()]=1;
	fo(k,1,n)fo(i,1,n)if (bz[i][k])
	fo(j,1,n)if (bz[k][j])bz[i][j]=1;
	fo(i,1,n)fo(j,1,n)if (bz[i][j])a[i][++a[i][0]]=j;
	fo(i,1,n)
	{
		memset(flag,1,sizeof(flag));
		if (find(i))++ans;
	}
	printf("%lld
",n-ans);
	return 0;
}