「学习笔记」泰勒级数

多项式函数是长这样的函数：

[f(x)=a_0+a_1x+a_2x^2+ldots+a_nx^n ]

它有一个很(Nice)的特点：代人(x)，在(O(n))的时间内就可以求出(f(x))，没有任何障碍.

但是这样的函数：

[g(x)=e^x ]

[h(x)=sin;x ]

想得到(g(3))或是(h(7))就比较困难了。因此我们需要用多项式函数去"取代"这些奇怪的函数。

逼近(f(x)=e^x)在x靠近0时的函数值

step1：用(y=a_0+a_1x)去逼近它.

具体的方法是让它的斜率等于(f(x))在(x=0)时的导数：1

让直线过((0,1))，于是得到的直线(y=x+1)

效果如下图：

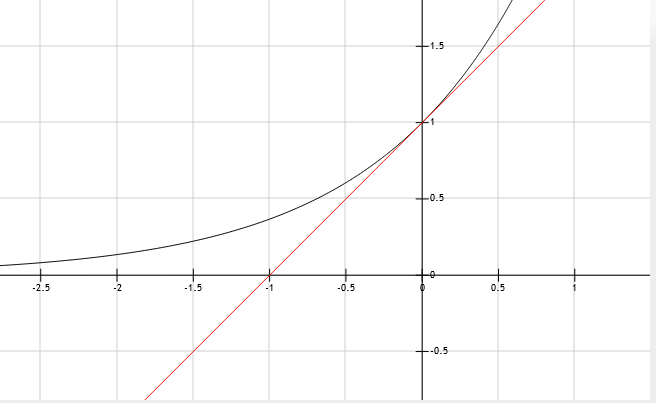
在(x)离(0)很近的时候还是比较精确的.

step2：用(g(x)=a_0+a_1x+a_2x^2)这个二次多项式去逼近它.

具体方法是让它在(x=0)处的函数值、导数值、二阶导数值与(f(x))相等.

[f(x)=e^x,f(0)=1 ]

[f'(x)=e^x,f'(0)=1 ]

[f''(x)=e^x,f''(0)=1 ]

再看这个二次多项式：

[g(x)=a_0+a_1x+a_2x^2,g(0)=a_0 ]

[g'(x)=a_1+2a_2x,g'(0)=a_1 ]

[g''(x)=2a_2,g''(0)=2a_2 ]

因为要让(f(x),f'(x),f''(x))与(g(x),g'(x),g''(x))分别对应相等，所以：

[a_0=1,a_1=1,2a_2=1 ]

所以(g(x)=1+x+frac{x^2}{2})

效果如下图.

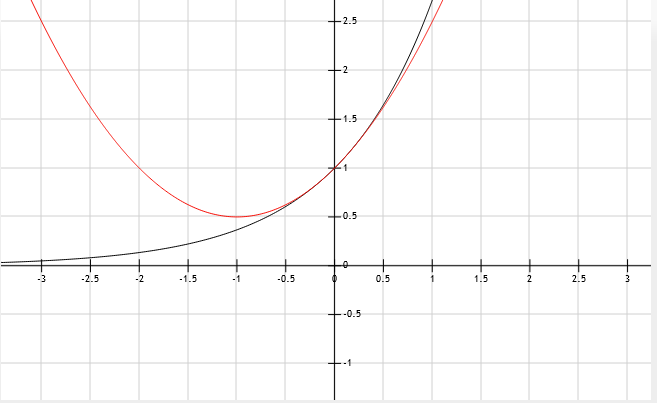
已经非常接近了呢.

step3：用(g(x)=a_0+a_1x+a_2x^2+a_3)这个三次多项式去逼近它.

具体方法是让它在(x=0)处的函数值、导数值、二阶导数值、三阶导数值与(f(x))相等.

[f(x)=e^x,f(0)=1 ]

[f'(x)=e^x,f'(0)=1 ]

[f''(x)=e^x,f''(0)=1 ]

[f'''(x)=e^x,f'''(0)=1 ]

再看这个三次多项式：

[g(x)=a_0+a_1x+a_2x^2+a_3x^3,g(0)=a_0 ]

[g'(x)=a_1+2a_2x+3a_2x^2,g'(0)=a_1 ]

[g''(x)=2a_2+,6a_3x,g''(0)=2a_2 ]

[g'''(x)=6a_3,g'''(0)=6a_3 ]

因为要让(f(x),f'(x),f''(x),f'''(x))与(g(x),g'(x),g''(x),g'''(x))分别对应相等，所以：

[a_0=1,a_1=1,2a_2=1,6a_3 ]

所以(g(x)=1+x+frac{x^2}{2}+frac{x^3}{6})

效果如下图.

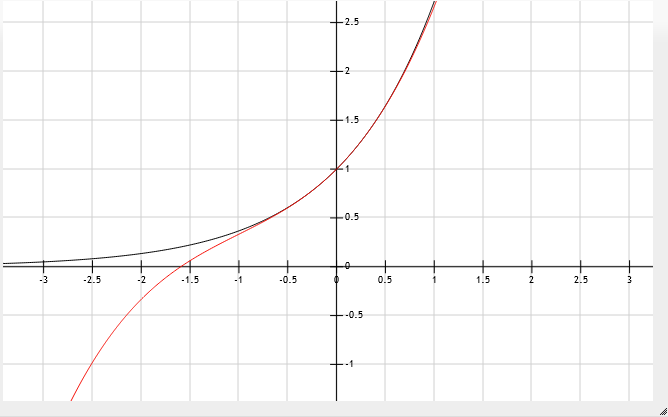
最后，推测得出结论:

[e^xapprox1+x+frac{x^2}{2!}+frac{x^3}{3!}+frac{x^4}{4!}+ldots ]

泰勒展开

一般来说，一个奇怪函数(f(x))，可以通过多项式函数(g(x))得到固定点(a)的近似值.(g(x))的形式是这样的：

[g(x)=b_0+b_1(x-a)+b_2(x-a)^2+b_3(x-a)^3+ldots+b_n(x-a)^n ]

经过和之前相似的一系列的推导（雾），得到了(famous)的公式：

泰勒逼近（泰勒展开）。

(f(x)approx f(a)+f'(a)(x-a)+frac{f''(a)}{2!}(x-a)^2+frac{f'''(a)}{3!}(x-a)^3+ldots+frac{f^{(n)}(a)}{n!}(x-a)^n)

把(a=0)代人，就得到了：

马克劳林逼近。

(f(x)approx f(0)+f'(0)x+frac{f''(0)}{2!}x^2+frac{f'''(0)}{3!}x^3+ldots+frac{f^{(n)}(0)}{n!}x^n)

泰勒级数的几个例子

泰勒公式基本就是这样了，下面是三个著名泰勒级数：

[e^x=1+x+frac{x^2}{2!}+frac{x^3}{3!}+frac{x^4}{4!}+ldots ]

[sin;x=x-frac{x^3}{3!}+frac{x^5}{5!}-ldots ]

[cos;x=1-frac{x^2}{2!}+frac{x^4}{4!}-ldots ]