Problem Description
Little A is an astronomy lover, and he has found that the sky was so beautiful!
So he is counting stars now!
There are n stars in the sky, and little A has connected them by m non-directional edges.
It is guranteed that no edges connect one star with itself, and every two edges connect different pairs of stars.
Now little A wants to know that how many different "A-Structure"s are there in the sky, can you help him?
An "A-structure" can be seen as a non-directional subgraph G, with a set of four nodes V and a set of five edges E.
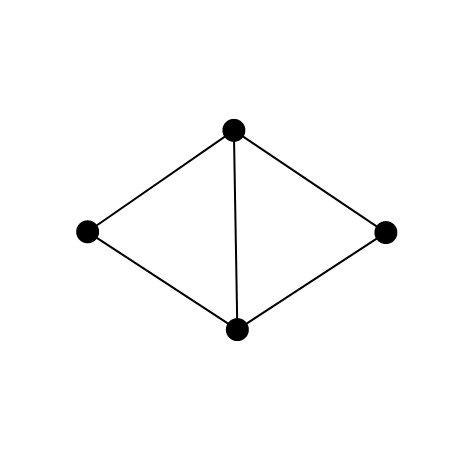
If V=(A,B,C,D) and E=(AB,BC,CD,DA,AC), we call G as an "A-structure".
It is defined that "A-structure" G1=V1+E1 and G2=V2+E2 are same only in the condition that V1=V2 and E1=E2.
Input
There are no more than 300 test cases.
For each test case, there are 2 positive integers n and m in the first line.
2≤n≤105, 1≤m≤min(2×105,n(n−1)2)
And then m lines follow, in each line there are two positive integers u and v, describing that this edge connects node u and node v.
1≤u,v≤n
∑n≤3×105,∑m≤6×105
Output
For each test case, just output one integer--the number of different "A-structure"s in one line.
Sample Input
4 5
1 2
2 3
3 4
4 1
1 3
4 6
1 2
2 3
3 4
4 1
1 3
2 4
Sample Output
1
6
Description(CHN)
给你一个图,找有多少个
Solution
三元环裸题
把每条边属于多少个三元环求出来,然后对于每条边算贡献就好了
如何求三元环,这是某道题目的solution的一部分

#include<bits/stdc++.h>
#define ui unsigned int
#define ll long long
#define db double
#define ld long double
#define ull unsigned long long
const int MAXN=300000+10,MAXM=600000+10;
int n,m,e,beg[MAXN],nex[MAXM<<1],to[MAXM<<1],cnt[MAXN],in[MAXN],arv[MAXN],pres[MAXN],clk;
struct node{
int u,v;
};
node side[MAXN];
ll ans=0;
template<typename T> inline void read(T &x)
{
T data=0,w=1;
char ch=0;
while(ch!='-'&&(ch<'0'||ch>'9'))ch=getchar();
if(ch=='-')w=-1,ch=getchar();
while(ch>='0'&&ch<='9')data=((T)data<<3)+((T)data<<1)+(ch^'0'),ch=getchar();
x=data*w;
}
template<typename T> inline void write(T x,char ch='�')
{
if(x<0)putchar('-'),x=-x;
if(x>9)write(x/10);
putchar(x%10+'0');
if(ch!='�')putchar(ch);
}
template<typename T> inline void chkmin(T &x,T y){x=(y<x?y:x);}
template<typename T> inline void chkmax(T &x,T y){x=(y>x?y:x);}
template<typename T> inline T min(T x,T y){return x<y?x:y;}
template<typename T> inline T max(T x,T y){return x>y?x:y;}
inline void insert(int x,int y)
{
to[++e]=y;
nex[e]=beg[x];
beg[x]=e;
}
int main()
{
while(scanf("%d%d",&n,&m)!=EOF)
{
e=ans=0;clk=1;
for(register int i=1;i<=n;++i)beg[i]=in[i]=arv[i]=pres[i]=0;
for(register int i=1,u,v;i<=m;++i)
{
cnt[i]=0;
read(u);read(v);
side[i].u=u;side[i].v=v;
in[u]++;in[v]++;
}
for(register int i=1,u,v;i<=m;++i)
{
u=side[i].u,v=side[i].v;
if(in[v]>in[u]||(in[v]==in[u]&&v>u))insert(u,v);
else insert(v,u);
}
for(register int i=1,u,v;i<=m;++i,++clk)
{
u=side[i].u,v=side[i].v;
for(register int j=beg[u];j;j=nex[j])arv[to[j]]=clk,pres[to[j]]=j;
for(register int j=beg[v];j;j=nex[j])
if(arv[to[j]]==clk)cnt[i]++,cnt[j]++,cnt[pres[to[j]]]++;
}
for(register int i=1;i<=m;++i)ans+=1ll*cnt[i]*(cnt[i]-1)/2;
write(ans,'
');
}
return 0;
}