行列式技巧

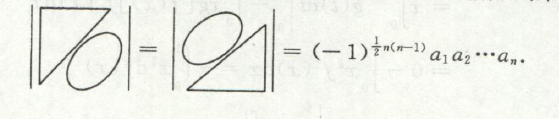
爪形行列式，用每一列乘以相应倍数加到第1列，将其第1行下方的行都化为0，得到上三角
然后主对角线元素相乘即可

范德蒙行列式

行列式化简可用行列交替
可利用行列式展开定理降阶
矩阵一般用行变换
只有特殊情况才用列变换
求梯矩阵或行简化梯矩阵:只用行变换
求等价标准形 可混用
解矩阵方程(XA=B):只用列变
解矩阵方程(AX=B):只用行变
求矩阵的逆:只用行变
求极大无关组:只用行变
求线性表示:只用行变
矩阵的秩:可混用
解线性方程组:基本上只用行变换; (列变换只在理论证明时用一下,目的是调换未知量的顺序)

为元素的代数余子式。

 

 

一般的分块矩阵的逆没有公式
对特殊的分块矩阵有:
diag(A1,A2,...,Ak)^-1 = diag(A1^-1,A2^-1,...,Ak^-1).
斜对角形式的分块矩阵如:
0 A
B 0
的逆 =
0 B^-1
A^-1 0
可推广.
A B
0 D
的逆 =
A^-1 -A^-1BD^-1
0 D^-1
A 0
C D
的逆 =
A^-1 0
D^-1CA^-1 D^-1

 两个矩阵乘积的秩bai满足的不等式如下：

1、r(A)≤dumin(m，n)≤zhim，n。

2、r(kA+lB)≤r(A)+r(B)。

3、r(AB)≤min(r(A)，r(B)) ≤r(A)。

4、r(ABC)≥r(AB)+r(BC)-r(B)。

5、r(AC)≥r(A) +r(C) -n上推dao，令B=In。

可以看出是两个矩阵乘积的秩也就是其中一个矩阵的秩减去另一个矩阵比满秩矩阵少的秩

6、r(kA+lB)-n≤r(A)+r(B)-n≤r(AB)≤min(r(A)，r(B))≤r(A)。

 

 可以看出矩阵等价则双方的基底可以互相表示

 实对称矩阵不同特征值的特征向量相互正交，三阶矩阵有其中两个可以推第三个