求e^x*sinx的不定积分

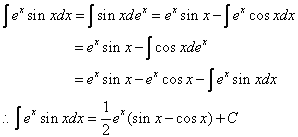
 扩展资料：

1、分部积分法的形式

（1）通过对u(x)求微分后，du=u'dx中的u'比u更加简洁。

例：∫x^2*e^xdx=∫x^2de^x=x^2*e^x-∫e^xdx^2=x^2*e^x-∫2x*e^xdx

（2）通过对u(x)求微分后使其类型与v(x)的类型相同或相近。

例：∫xarctanxdx=∫arctanxd(1/2x^2)

=1/2x^2*arctanx-1/2∫x^2darctanx=1/2x^2*arctanx-1/2∫x^2/(1+x^2)dx

（3）利用有些函数经一次或二次求微分后不变的性质来进行分部积分。

例：∫e^x*sinxdx=∫sinxde^x=e^x*sinx-∫e^xdsinx=e^x*sinx-∫e^x*cosxdx

=e^x*sinx-∫cosxde^x=e^x*sinx-e^x*cosx+∫e^xdcosx

=e^x*sinx-e^x*cosx-∫e^x*sinxdx

则2∫e^x*sinxdx=e^x*sinx-e^x*cosx，可得

∫e^x*sinxdx=1/2e^x*（sinx-cosx）+C

分部积分：

(uv)'=u'v+uv'，得：u'v=(uv)'-uv'。

两边积分得：∫ u'v dx=∫ (uv)' dx - ∫ uv' dx。

即：∫ u'v dx = uv - ∫ uv' d,这就是分部积分公式。

也可简写为：∫ v du = uv - ∫ u dv。

常用积分公式：

1）∫0dx=c

2）∫x^udx=(x^(u+1))/(u+1)+c

3）∫1/xdx=ln|x|+c

4）∫a^xdx=(a^x)/lna+c

5）∫e^xdx=e^x+c

6）∫sinxdx=-cosx+c

7）∫cosxdx=sinx+c

8）∫1/(cosx)^2dx=tanx+c

9）∫1/(sinx)^2dx=-cotx+c

10）∫1/√（1-x^2) dx=arcsinx+c

11）∫1/(1+x^2)dx=arctanx+c