梯度下降法

转自：http://www.cnblogs.com/Sinte-Beuve/p/6164689.html

本文主要讲了梯度下降法的两种迭代思路，随机梯度下降（Stochastic gradient descent）和批量梯度下降（Batch gradient descent）。以及他们在python中的实现。

梯度下降法

梯度下降是一个最优化算法，通俗的来讲也就是沿着梯度下降的方向来求出一个函数的极小值。那么我们在高等数学中学过，对于一些我们了解的函数方程，我们可以对其求一阶导和二阶导，比如说二次函数。可是我们在处理问题的时候遇到的并不都是我们熟悉的函数，并且既然是机器学习就应该让机器自己去学习如何对其进行求解，显然我们需要换一个思路。因此我们采用梯度下降，不断迭代，沿着梯度下降的方向来移动，求出极小值。

此处我们还是用coursea的机器学习课中的案例，假设我们从中介那里拿到了一个地区的房屋售价表，那么在已知房子面积的情况下，如何得知房子的销售价格。显然，这是一个线性模型，房子面积是自变量x，销售价格是因变量y。我们可以用给出的数据画一张图。然后，给出房子的面积，就可以从图中得知房子的售价了。

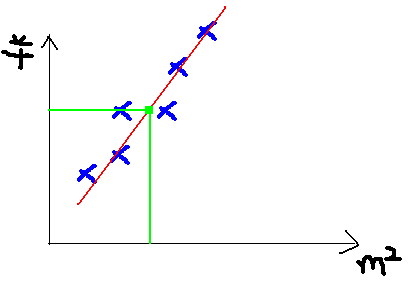
现在我们的问题就是，针对给出的数据，如何得到一条最拟合的直线。

对于线性模型，如下。

• h(x)是需要拟合的函数。
• J(θ)称为均方误差或cost function。用来衡量训练集众的样本对线性模式的拟合程度。
• m为训练集众样本的个数。
• θ是我们最终需要通过梯度下降法来求得的参数。

 

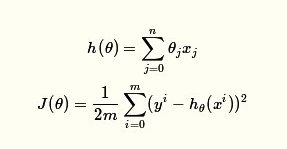
接下来的梯度下降法就有两种不同的迭代思路。

批量梯度下降（Batch gradient descent）

现在我们就要求出J(θ)取到极小值时的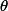θT 向量。之前已经说过了，沿着函数梯度的方向下降就能最快的找到极小值。

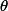
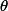1. 计算J(θ)关于θT 的偏导数,也就得到了向量中每一个θ 的梯度。
   
   
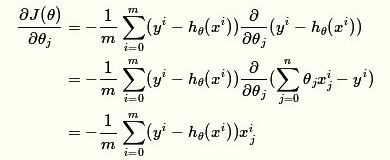
2. 沿着梯度的方向更新参数θ的值
   
   
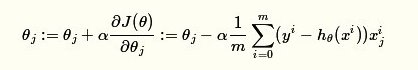
3. 迭代直到收敛。

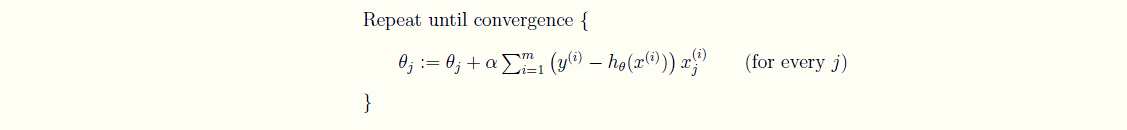
可以看到，批量梯度下降是用了训练集中的所有样本。因此在数据量很大的时候，每次迭代都要遍历训练集一遍，开销会很大，所以在数据量大的时候，可以采用随机梯度下降法。

随机梯度下降（Stochastic gradient descent）

和批量梯度有所不同的地方在于，每次迭代只选取一个样本的数据，一旦到达最大的迭代次数或是满足预期的精度，就停止。

可以得出随机梯度下降法的θ更新表达式。

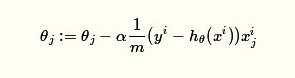
迭代直到收敛。

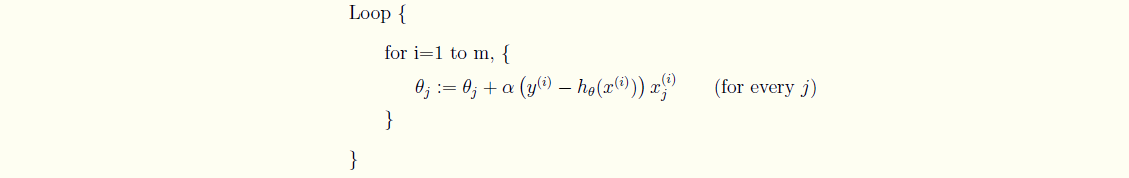
两种迭代思路的python实现

下面是python的代码实现，现在仅仅是用纯python的语法（python2.7）来实现的。随着学习的深入，届时还会有基于numpy等一些库的实现，下次补充。

#encoding:utf-8

#随机梯度
def stochastic_gradient_descent(x,y,theta,alpha,m,max_iter):
    """随机梯度下降法，每一次梯度下降只使用一个样本。

    :param x: 训练集种的自变量
    :param y: 训练集种的因变量
    :param theta: 待求的权值
    :param alpha: 学习速率
    :param m: 样本总数
    :param max_iter: 最大迭代次数
    """
    deviation = 1
    iter = 0    
    flag = 0
    while True:
        for i in range(m):  #循环取训练集中的一个
            deviation = 0
            h = theta[0] * x[i][0] + theta[1] * x[i][1]
            theta[0] = theta[0] + alpha * (y[i] - h)*x[i][0] 
            theta[1] = theta[1] + alpha * (y[i] - h)*x[i][1]

            iter = iter + 1
            #计算误差
            for i in range(m):
                deviation = deviation + (y[i] - (theta[0] * x[i][0] + theta[1] * x[i][1])) ** 2
            if deviation <EPS or iter >max_iter:
                flag = 1 
                break
        if flag == 1 :
            break   
    return theta, iter

#批量梯度
def batch_gradient_descent(x,y,theta,alpha,m,max_iter):
    """批量梯度下降法，每一次梯度下降使用训练集中的所有样本来计算误差。

    :param x: 训练集种的自变量
    :param y: 训练集种的因变量
    :param theta: 待求的权值
    :param alpha: 学习速率
    :param m: 样本总数
    :param max_iter: 最大迭代次数
    """
    deviation = 1
    iter = 0
    while deviation > EPS and iter < max_iter:
        deviation = 0
        sigma1 = 0
        sigma2 = 0
        for i in range(m): #对训练集中的所有数据求和迭代
            h = theta[0] * x[i][0] + theta[1] * x[i][1]
            sigma1 = sigma1 +  (y[i] - h)*x[i][0] 
            sigma2 = sigma2 +  (y[i] - h)*x[i][1] 
        theta[0] = theta[0] + alpha * sigma1 /m
        theta[1] = theta[1] + alpha * sigma2 /m
        #计算误差
        for i in range(m):
            deviation = deviation + (y[i] - (theta[0] * x[i][0] + theta[1] * x[i][1])) ** 2
        iter = iter + 1
    return theta, iter


#运行 为两种算法设置不同的参数
# data and init 
matrix_x = [[2.1,1.5],[2.5,2.3],[3.3,3.9],[3.9,5.1],[2.7,2.7]]
matrix_y = [2.5,3.9,6.7,8.8,4.6]
MAX_ITER = 5000
EPS = 0.0001 

#随机梯度
theta = [2,-1]
ALPHA = 0.05

resultTheta,iters = stochastic_gradient_descent(matrix_x, matrix_y, theta, ALPHA, 5, MAX_ITER)
print 'theta=',resultTheta
print 'iters=',iters

#批量梯度
theta = [2,-1]
ALPHA = 0.05

resultTheta,iters = batch_gradient_descent(matrix_x, matrix_y, theta, ALPHA, 5, MAX_ITER)
print 'theta=',resultTheta
print 'iters=',iters

总结

梯度下降法是一种最优化问题求解的算法。有批量梯度和随机梯度两种不同的迭代思路。他们有以下的差异：

• 批量梯度收敛速度慢，随机梯度收敛速度快。
• 批量梯度是在θ更新前对所有样例汇总误差，而随机梯度下降的权值是通过考查某个样本来更新的
• 批量梯度的开销大，随机梯度的开销小。

使用梯度下降法时需要寻找出一个最好的学习效率。这样可以使得使用最少的迭代次数达到我们需要的精度。