六个常见函数的图像
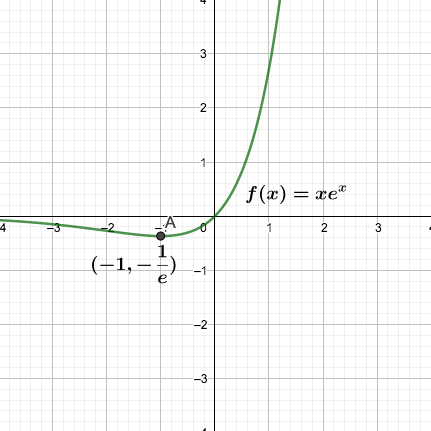


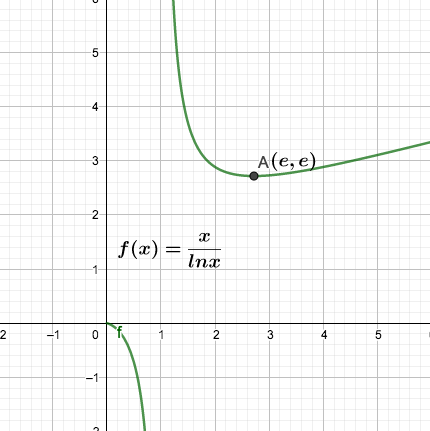
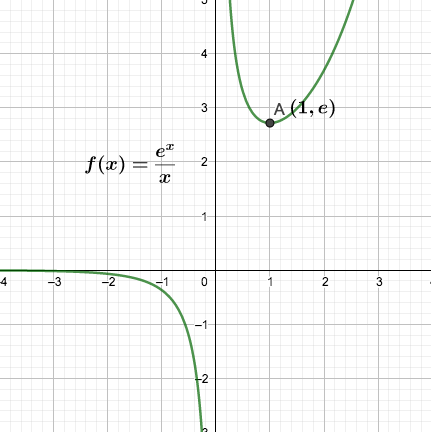
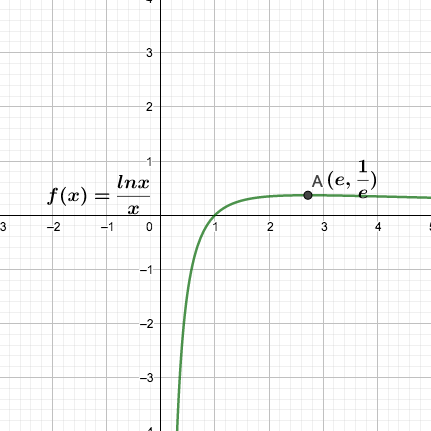
$e^x$的泰勒展开:
$$e^x= sum_{i=0}^{+infty} frac{x^i}{i!} =1 + x + frac{x^2}{2!} + frac{x^3}{3!} + ··· + frac{x^n}{n!} + o(x^n)$$
因此有$$e^x geq x + 1 (x in R)$$
也就是$$x geq ln x + 1 (x>0)$$
代换一下$$frac{1}{e^x} geq 1 - x \ ln x geq 1 - frac{1}{x}$$
当然也有(尽管目前从没见过)$$e^x geq frac{1}{2}x^2 + x + 1 (x>0)$$
一种变形
$$x^2e^x=e^{x+2 ln x} geq x+2 ln x+1 或 xe^{2x}=e^{2x+ ln x} geq 2x+ ln x+1$$
同理还有$ln (x+1)$的泰勒展开
诡异放缩:$$e^x>x^2$$或$$ln x <sqrt{x}$$
三角函数的分段放缩
$0<x<1$时,放到$x$
$$x>sin x (x>0)$$
$x>1$时,放到$±1$
$$-1 leq sin x leq 1$$
此外$0<x<dfrac{pi}{2}$时 $$sin x < x < an x$$
基本不等式放缩
可处理根式$$sqrt{x+1} = sqrt{(x+1) imes 1} < frac{(x+1)+1}{2} = frac{x}{2} + 1$$
柯西不等式放缩(或求最值)
例如$dfrac{x+1}{sqrt{x^2+2}} = dfrac{x+1}{sqrt{dfrac{2}{3} (x^2+2) (1+dfrac{1}{2})}} le sqrt{dfrac{3}{2}} = dfrac{sqrt{6}}{2}$