逆序对

仔细想想，如果存在正整数 i, j 使得 1 ≤ i < j ≤ n 且 A[i] > A[j]，则称为一个逆序对。 这就意味着如果想要统计逆序对，就要在数列中 从左向右依次算出 每个数右侧比自己小的数的个数，最后将将其相加。但是，当我们新读入一个数时，根本不清楚后面还未读进来的数是怎样的！

所以对于此类问题，有两种解决方案：

1. 从右向左读取 统计已经读取的数中比自己小的个数。
2. 从左向右读取 统计已经读取的数中比自己大的个数。

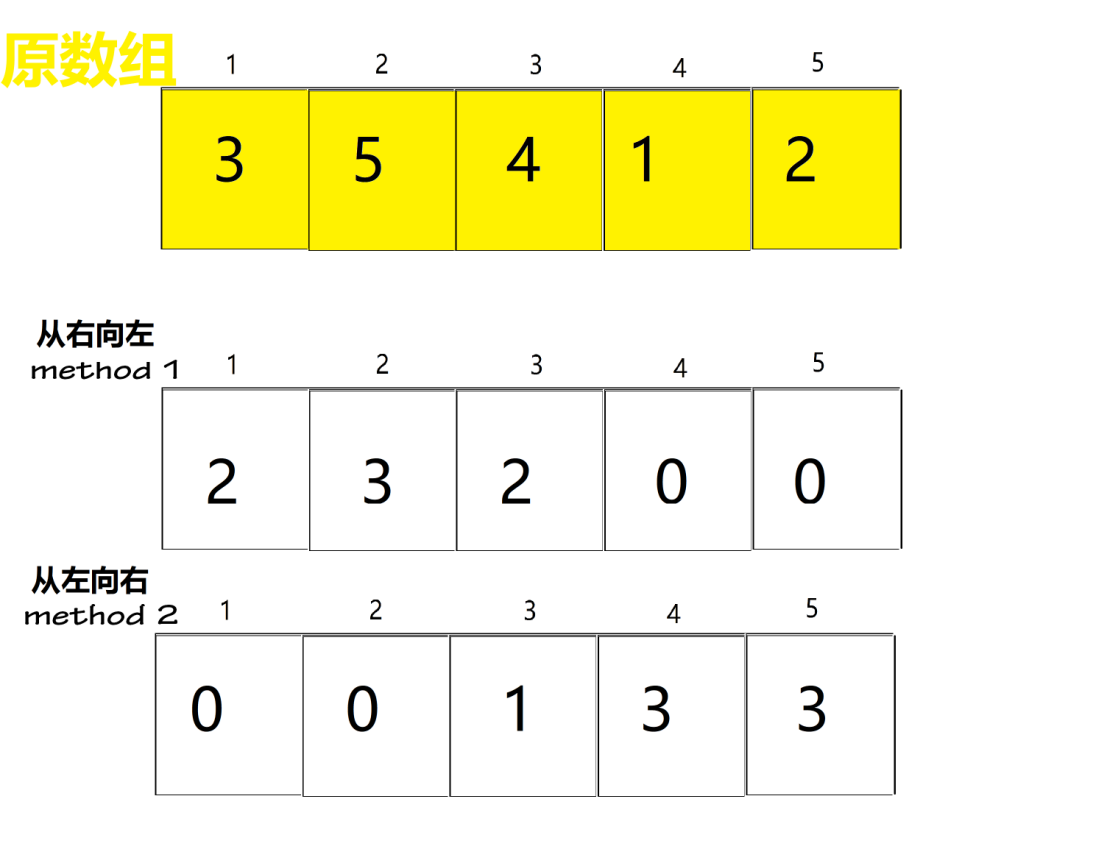
根据树状数组向上更新、向下查询的特性，我们更习惯用从右到左向上查询的方法。（其实从左到右向上查询也不是无法实现，只要求出顺序对个数 再用组合总数N*(N-1)/2减掉顺序对个数同样可以得到逆序对个数）

从右向左

#include<iostream>
#include<cstring>
using namespace std;
int n, a[100000], s[100000], sum=0;

int lowbit(int x){return x & -x;}
int update(int x, int y){
    for(; x<=n; x+=lowbit(x))
        s[x] += y;
}
int getsum(int x){
    int ans=0;
    for(; x; x-=lowbit(x))
        ans += s[x];
    return ans;
}

int main(){
    ios::sync_with_stdio(false);
    memset(a, 0, sizeof(a));
    memset(s, 0, sizeof(s));
    cin >> n;
    for(int i=1; i<=n; i++) cin >> a[i];
    
    for(int i=n; i>=1; i--){
        sum += getsum(a[i]);
        update(a[i], 1);
    }
    cout << sum << "
";
    return 0;
}

从左向右

#include<iostream>
#include<cstring>
using namespace std;
int n, a[100000], s[100000], sum=0;
int lowbit(int x){return x & -x;} 
int getsum(int x){
    int ans=0;
    for(; x<=n; x+=lowbit(x))
        ans += s[x];
    return ans;
}
int update(int x, int y){
    for(;x;x-=lowbit(x))
        s[x]+=y;
}

int main(){
    ios::sync_with_stdio(false);
    memset(a,0,sizeof(a));
    memset(s,0,sizeof(s));
    
    cin >> n;
    for(int i=1; i<=n; i++){
        cin >> a[i];
        sum+=getsum(a[i]);
        update(a[i],1);
    } 
    cout << sum << "
";
    
    return 0;
}