998. 起床困难综合症

原题链接：998. 起床困难综合症

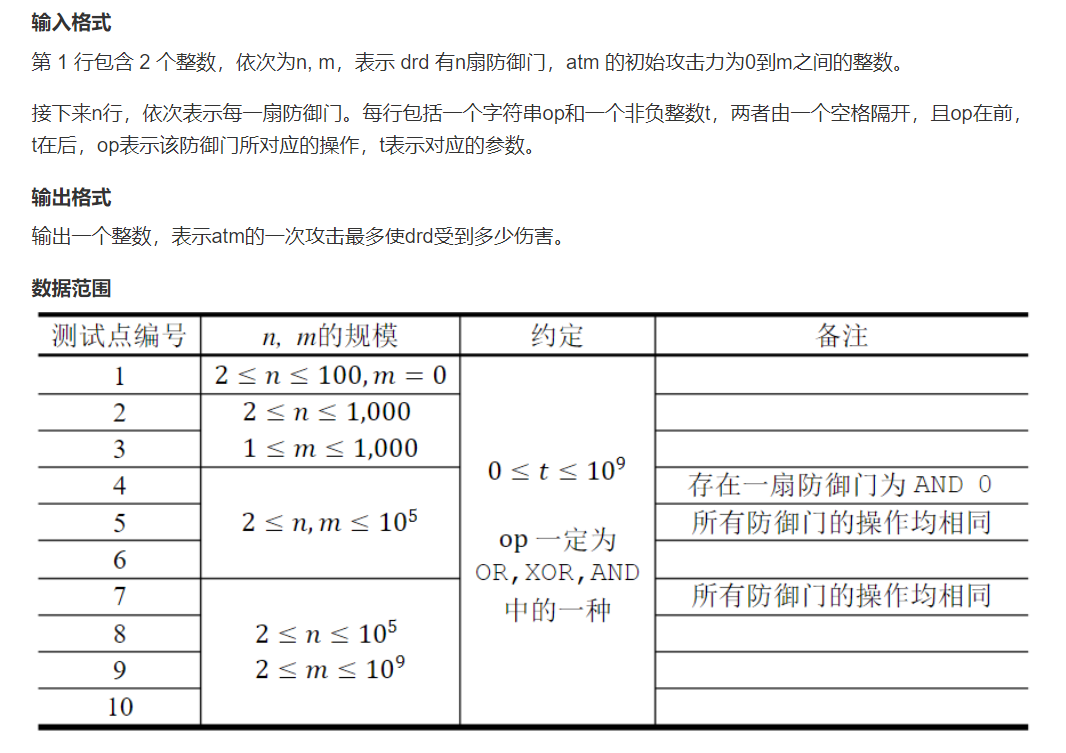
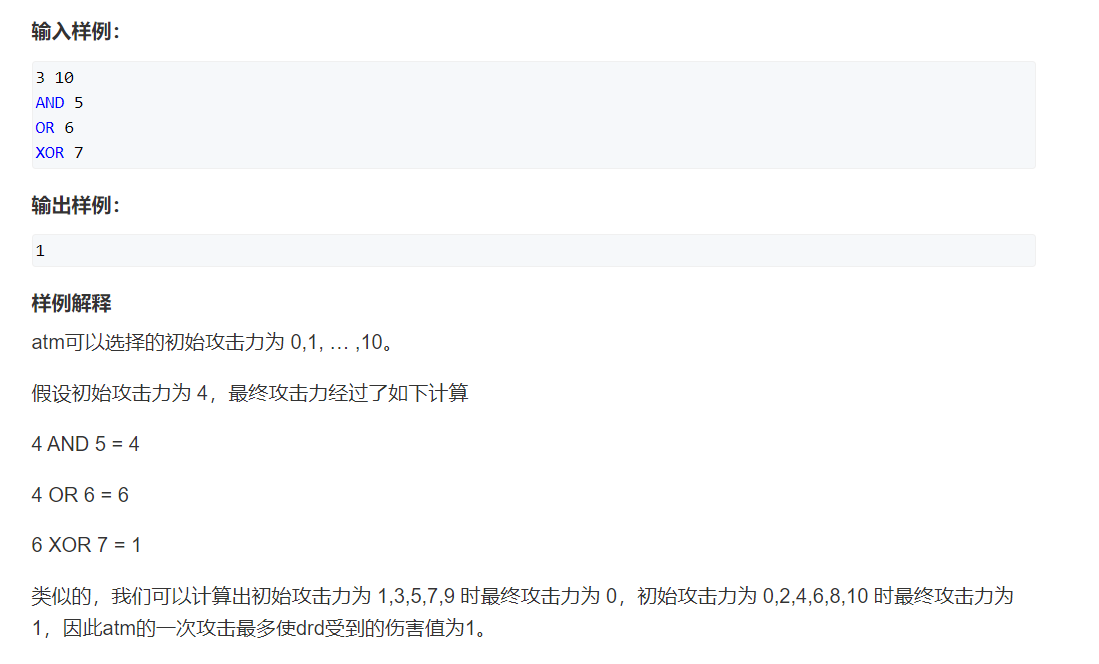
本题是让我们选择[0,m]之间的一个整数x，经过给定的n次位运算，使结果ans最大。
位运算的主要特点之一是在二进制表示下不进位。正因为如此，在x可以任意选择的情况下从，参与位运算的各个位(bit)之间是独立无关的。换言之，对于任意的k(0<=k<30)，“ans的第k位是几”只与“x的第k位是几”有关，与其他位无关。所以我们可以从高位到低位，依次考虑x的每一位填0或者填1。

x的第k位应该填1，当且仅当同时满足以下两个条件：
1.已经填好的更高位数构成的数值加上1<<k以后不超过m。
2.用每个参数的第k位参与位运算。若初值为1，则n次位运算后结果为1：若初值为0，则n次位运算后结果为0。

如果不满足上述条件，要么填1会超过m的范围，要么填1不如填0更优。这种情况下令x的第k位为0显然更好。确定x的每一位，自然可以得到ans的值

#include<bits/stdc++.h>
using namespace std;
int n,m;
pair<string,int> a[100005];
int calc(int bit,int now)
{
    for(int i=1;i<=n;i++)
    {
            int x=a[i].second>>bit&1;
        if(a[i].first=="AND")
            now&=x;
        else if(a[i].first=="OR")
            now|=x;
        else
            now^=x;
    }
    return now;
}
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        char str[5];
        int x;
        scanf("%s%d",str,&x);
        a[i]=make_pair(str,x);
    }
    int val=0,ans=0;
    for(int bit=29;bit>=0;bit--)
    {
        int res0=calc(bit,0);
        int res1=calc(bit,1);
        if(val+(1<<bit)<=m&&res0<res1)
            val+=1<<bit,ans+=res1<<bit;
        else
            ans+=res0<<bit;
    }
    cout<<ans<<endl;
    return 0;
}