题目链接:背包问题求具体方案

算法一
题目要求输出字典序最小的解,假设存在一个包含第1个物品的最优解,为了确保字典序最小那么我们必然要选第一个。那么问题就转化成从2~N这些物品中找到最优解。之前的f(i,j)记录的都是前i个物品总容量为j的最优解,那么我们现在将f(i,j)定义为从第ii个元素到最后一个元素总容量为j的最优解。接下来考虑状态转移:
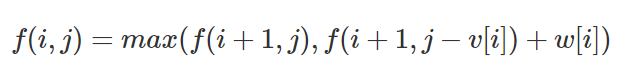
两种情况,第一种是不选第i个物品,那么最优解等同于从第i+1个物品到最后一个元素总容量为j的最优解;第二种是选了第i个物品,那么最优解等于当前物品的价值w[i]加上从第i+1个物品到最后一个元素总容量为j−v[i]的最优解。
计算完状态表示后,考虑如何的到最小字典序的解。首先f(1,m)肯定是最大价值,那么我们便开始考虑能否选取第1个物品呢。
如果f(1,m)=f(2,m−v[1])+w[1],说明选取了第1个物品可以得到最优解。
如果f(1,m)=f(2,m),说明不选取第一个物品才能得到最优解。
如果f(1,m)=f(2,m)=f(2,m−v[1])+w[1],说明选不选都可以得到最优解,但是为了考虑字典序最小,我们也需要选取该物品。
c++代码
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int f[N][N];
int v[N],w[N];
int n,m;
int main()
{
cin >> n >> m;
for(int i = 1 ; i <= n ; i++)
cin >> v[i] >> w[i];
for(int i = n ; i >= 1 ; i --)
{
for(int j = 0 ; j <= m ; j++)
{
f[i][j] = f[i + 1][j];
if(j >= v[i])
f[i][j] = max(f[i][j],f[i + 1][j - v[i]] + w[i]);
}
}
int cur_v = m;
for(int i = 1 ; i <= n ; i++)
{ //如果是最后一个元素,特判一下,防止越界即可
if(i == n && cur_v >= v[i])
{
printf("%d ",i);
break;
}
if(cur_v <= 0)
break;
//判断下标是否越界
if(cur_v - v[i]>=0 && f[i][cur_v] == f[i + 1][cur_v - v[i]] + w[i]){
printf("%d ",i);
cur_v = cur_v - v[i];//选了第i个物品,剩余容量就要减小。
}
}
return 0;
}
作者:T-SHLoRk
链接:https://www.acwing.com/solution/content/2687/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。