最近复习了隐函数的定义,发现以前真的只是在按模板套公式,没有理解这个隐函数的具体内含~
先贴一下隐函数的定义:
由于百度百科上的定义,个人感觉还不是很浅显得表达,所以下面贴一下同济教材得定义:

定义解释:其实就是说:y=x这种情况下得函数表达,就是显函数;而类似y-x=0这种表达就是隐函数。
求导法则有这些:

此处主要记录很多人没有理解清楚的方法2,对函数两边求导;
下面还是贴一下同济教材的习题给予说明:

解上面的题目需要了解两点知识:
(1)等式两边对X求导,是什么意思?
(2)什么情况下可以对两边求导,等式仍然成立?
一.解释第一个问题:等式两边对X求导,是什么意思?
前言:
要解决这个问题,首先要知道求导的意义在哪里,即为什么求导?
在生产生活中,我们要研究一件东西,或者某一件事情的情况,往往可以用函数来表达它,但是往往代数式的表达比较抽象,不够直观,所以引入了几何图象,数形结合,有了更直观的感受。所以当我们把一件事物通过函数图像描述出来以后,我们往往需要更进一步的信息,比如这个图像的增减情况的波动情况如何,所以就引入了导数,导数在研究一个连续的图像的时候往往非常有效,它可以表达这件事务的波动情况,对事物进行更好的描述。
了解了为什么求导,这就增强了我们学习的动力,因为求导可以方便我们的各项工作。接下来解释;两边对X求导的意思。
1.分析下这句话的关键词,“两边”,“对X”,"求导"。
1.1首先分析求导的概念:求导,对于函数来说就是求它的导函数,导函数可以描述这个函数在定义区间里的每一点的斜率;对于某个点来说,就是求它在这点的切线斜率。
很显然,这里我们要对隐函数求导,当然是求它的导函数(简称导数)。
1.2解释“对X”这个词的含义,对X,意思言简意赅,就是研究X这个对象。
1.3“两边”,意思很浅显,就是两边都顾及到。
2.把这句话串起来解释
2.1等式两边对X求导,意思就是说,等式两边都要对X这个对象进行求导,好了,这句话解释完了,就这么简单。但是往往这样解释还不够浅显~
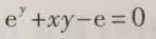
因为对这个函数来说,同学们都有这个疑惑,因为答案是这样的:
对于左边求导: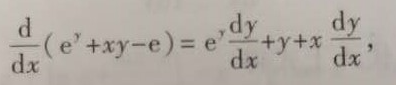
对于右边求导: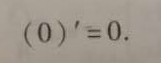
这个疑惑点在哪里?其实就是题目的直观理解与解题过程的理解的偏差。
e^y为什么可以写成e^y(dy/dx), xy为什么写成:y+x(dy/dx), 为什么e^y与x没有关系,它却可以求导,并且写出来等于e^y(dy/dx),而e却消失不见!
2.2进一步解释
其实对上面这个过程感觉困惑的原因在于,没有好好的理解隐函数的定义,那么我们会过头来看看定义:

说白了就是说,对于任意X,总能找到唯一的y。所以我们应该这样看待y,对于所有含y的表达式,我们都把它看成于x相关联的存在,也就是说把y看成x的复合函数,这里就不解释复合函数的概念了,因为相信读者自己明白这个小概念。
所以根据复合函数的求导法则,就可以知道e^y求导后,写成e^y(dy/dx);而对于xy求导,利用分部积分的概念xy=x'y+xy', x对x求导就是1,而y需要看成x的复合函数的形式,所以y'=(dy/dx),而e与x没有关系,不可以写成x的任何形式,所以就等于0,舍去。同理,左边的0,0关于x求导还是0.
注:可能很多人对y关于X求导就等于(dy/dx)不是很清楚,其实这个表达式就是导数的定义了,其意义就是,y的增量/x的增量 = 函数y的斜率,补上这一句,应该就解释得差不多了。
二.解释第二个问题:什么情况下可以对两边求导,等式仍然成立?
其实这个两边求导,等式仍然成立是有要求的,同济教材也有特意指出,不然就很容易产生谬误~
它里面注释是这么说的

所以说白了,对两边求导是要建立在恒等式下的。
其实这句话隐含表达了两个意思:
你要对等式两边对X求导,首先要满足以下条件:
(1)函数条件下,首先你得是个函数才可以求导。(这句话看似废话,其实很有用)
(2)在满足(1)的条件下,不管x取何值,都要满足等式始终成立。
好了这里就解释清楚了,至于我为什么要解释第二个问题,感觉好像没什么用处,你看我下面的举例就明白了。
例子:对于X= 3,是否可以两边对X求导?
我们对左边X求导:X'=1;
对右边求导:3'=0;
糟了,不是说对于恒等式来说,两边求导不是相等吗,啊,我好紧张啊,我好像推翻了一个伟大的数学定义,莫非我要出名了?诺奖下一个是我吗?我可要做好获奖感言……
首先,我的回答是:梦里啥都有,挺好的~
现在分析我们理解的谬误:
首先呢,X=3的确是一个等式,但是它却不是一个函数,因为确定了X,并不可以找到另一个变量y,与它形成映射关系,说白了这玩意就是一个单纯的方程而已,它不构成函数!
还有,再补充一点,其实可以求导的函数都是拥有两个及两个变量以上的函数式子。单单举例X-Y=3,来说对这个等式求导,其实这个最简单形式的函数已经有两个变量了,所以一个变量的式子何来映射关系,更不可能形成函数了!