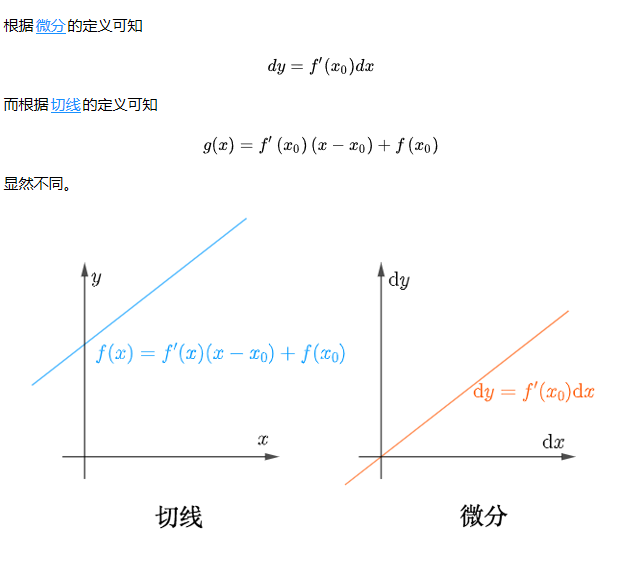
首先呢,导数是一个比值,是y增量与x增量的比值;而微分呢,是一个增量,dx=x的增量,dy=y的增量,近似看成函数在y轴上的增量。
看看维基百科:
微分定义

导数定义

(1)导数与导函数;
首先呢,导数是一个比值,也就是一个数,可以想象成一个点;
导函数是函数,是点的集合。
(2)微分函数 与 函数的微分
这两个家伙可比上面的导函数与导数更容易混淆!
函数微分的定义:

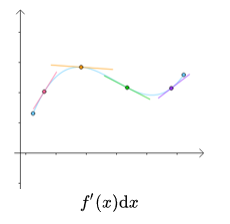
dy = A*X增量 === f'(X)dX
其中 A === f'(X) X增量 === dX 所以依笔者看来,函数的微分其实可以看成这个函数可以分解成无数个切点,也就是说所有点都对应着一个切线函数。它是针对所有点来说,都有切线函数
---------------------------------------------------------------------------------------------------------------
微分函数f'(X0)dX的定义
其实网上我没找到它的定义。下面是我在其它地方看到的题目,下面的题目把微分函数表达为一个函数。你可以把微分函数理解成原函数在某点的切线函数,只不过这个切线函数是换了坐标的,换坐标的切线函数一定经过原点,所以它就有了另一个名字,微分函数。它是针对于一个点来说的切线函数。