Codeforces 500B New Year Permutation( Floyd + 贪心 )

B. New Year Permutation

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

User ainta has a permutation p1, p2, ..., pn. As the New Year is coming, he wants to make his permutation as pretty as possible.

Permutation a1, a2, ..., an is prettier than permutation b1, b2, ..., bn, if and only if there exists an integer k (1 ≤ k ≤ n) where a1 = b1, a2 = b2, ..., ak - 1 = bk - 1 and ak < bk all holds.

As known, permutation p is so sensitive that it could be only modified by swapping two distinct elements. But swapping two elements is harder than you think. Given an n × n binary matrix A, user ainta can swap the values of pi and pj (1 ≤ i, j ≤ n, i ≠ j) if and only if Ai, j = 1.

Given the permutation p and the matrix A, user ainta wants to know the prettiest permutation that he can obtain.

Input

The first line contains an integer n (1 ≤ n ≤ 300) — the size of the permutation p.

The second line contains n space-separated integers p1, p2, ..., pn — the permutation p that user ainta has. Each integer between 1 and n occurs exactly once in the given permutation.

Next n lines describe the matrix A. The i-th line contains n characters '0' or '1' and describes the i-th row of A. Thej-th character of the i-th line Ai, j is the element on the intersection of the i-th row and the j-th column of A. It is guaranteed that, for all integers i, j where 1 ≤ i < j ≤ n, Ai, j = Aj, i holds. Also, for all integers i where 1 ≤ i ≤ n, Ai, i = 0 holds.

Output

In the first and only line, print n space-separated integers, describing the prettiest permutation that can be obtained.

Sample test(s)

input

7
5 2 4 3 6 7 1
0001001
0000000
0000010
1000001
0000000
0010000
1001000

output

1 2 4 3 6 7 5

input

5
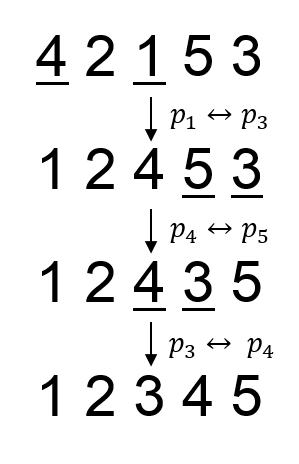
4 2 1 5 3
00100
00011
10010
01101
01010

output

1 2 3 4 5

Note

In the first sample, the swap needed to obtain the prettiest permutation is: (p1, p7).

In the second sample, the swaps needed to obtain the prettiest permutation is (p1, p3), (p4, p5), (p3, p4).

                                           

A permutation p is a sequence of integers p1, p2, ..., pn, consisting of n distinct positive integers, each of them doesn't exceed n. The i-th element of the permutation p is denoted as pi. The size of the permutation p is denoted as n.

题意：序列 a1, a2, ..., an ， b1, b2, ..., bn, 如果存在整数 k (1 ≤ k ≤ n) 符合 a1 = b1, a2 = b2, ..., ak - 1 = bk - 1 并且 ak < bk .

则称 a 序列比 b序列好。

题目给出一个序列 p ，再给出一个n*n的矩阵A ， A[i][j] = 1 ，表示p中第i个元素能跟第j个元素交换 。

问p经过交换后，最好的序列是什么。

做法是用Floyd先处理任意pi , pj 能否交换 O（n^3）

然后再将序列从前到后贪心交换一次。

#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int n , a[N] , A[N][N];
string s ;
int main()
{
    cin >> n;
    for( int i = 1 ; i <= n ; ++i ) cin >> a[i];
    for( int i = 1 ; i <= n ; ++i ) {
        cin >> s ;
        for( int j = 0 ; j < n ; ++j ){
            if( s[j] == '1' ) A[i][j+1] = 1 ;
            else A[i][j+1] = 0 ;
        }
    }
    for( int i = 1 ; i <= n ; ++i ){
        for( int j = 1 ; j <= n ; ++j ){
            if( A[j][i] == 0 ) continue ;
            for( int k = 1 ; k <= n ; ++k ){
                if( A[i][k] ) A[j][k] = 1 ;
            }
        }
    }

    for( int i = 1 ; i <= n ; ++i ){
        for( int j = i + 1 ; j <= n ; ++j ){
            if( A[i][j] && a[i] > a[j] ) swap( a[i] , a[j] );
        }
    }
    for( int i = 1 ; i <= n ; ++i ) cout << a[i] << ' ';
}