题目描述
尼克每天上班之前都连接上英特网,接收他的上司发来的邮件,这些邮件包含了尼克主管的部门当天要完成的全部任务,每个任务由一个开始时刻与一个持续时间构成。
尼克的一个工作日为N分钟,从第一分钟开始到第N分钟结束。当尼克到达单位后他就开始干活。如果在同一时刻有多个任务需要完成,尼克可以任选其中的一个来做,而其余的则由他的同事完成,反之如果只有一个任务,则该任务必需由尼克去完成,假如某些任务开始时刻尼克正在工作,则这些任务也由尼克的同事完成。如果某任务于第P分钟开始,持续时间为T分钟,则该任务将在第P+T-1分钟结束。
写一个程序计算尼克应该如何选取任务,才能获得最大的空暇时间。
输入输出格式
输入格式
输入数据第一行含两个用空格隔开的整数N和K(1≤N≤10000,1≤K≤10000),N表示尼克的工作时间,单位为分钟,K表示任务总数。
接下来共有K行,每一行有两个用空格隔开的整数P和T,表示该任务从第P分钟开始,持续时间为T分钟,其中1≤P≤N,1≤P+T-1≤N。
输出格式
输出文件仅一行,包含一个整数,表示尼克可能获得的最大空暇时间。
样例
INPUT
15 6
1 2
1 6
4 11
8 5
8 1
11 5
OUTPUT
4
HINT
SOLUTION
dp
这题的转移方式非常简单,就是两个式子:
当前时刻没有工作开始我们就从前一个时刻转移:(dp[i]=dp[i+1]+1)
当前时刻有工作开始我们从所有(以当前时刻为开始时刻的工作的)结束时间(区间对应的(r))转移:(dp[i]=Max(dp[i],dp[i+len]))((i+len)就是前文的(r))。
这里按这种转移方式的话,我们是应该逆着转移的。
然后我就怎么也想不明白为什么不能顺着推。花了我一下午,qwq。
如图:
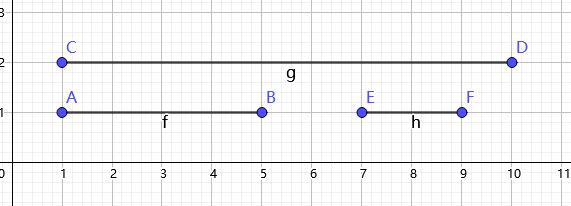
你看上面的线段,如果我顺着推的话,我们由AB,EF组成的更优的答案就会被CD在转移过程中覆盖掉,但是在逆着推的情况下,我们AB,EF组成的答案就会作为更优解被保留下来。
对就是这样qwq。
总而言之,对于每一个任务结束时的情况我们是不能覆盖掉的,最优解只能从不同任务结束时转移而来,因为我们这一题的本来就是要在空闲时遇到任务就必须要接任务,但是又没有规定任务结束的时间。
换而言之,我们的答案是沿着我们规定的方向转移来的,但是,最先开始的任务规定了一定要接,而没有任何规定说最后结束的任务一定要接,所以我们的解一定会包含最开始的任务,却不一定会包含最后结束的任务,这就是区别。