小波去噪基本概念 -转

https://blog.csdn.net/qq_40587575/article/details/83188527

一、前言

     在现实生活和工作中，噪声无处不在，在许多领域中，如天文、医学图像和计算机视觉方面收集到的数据常常是含有噪声的。噪声可能来自获取数据的过程，也可能来自环境影响。由于种种原因,总会存在噪声，噪声的存在往往会掩盖信号本身所要表现的信息，所以在实际的信号处理中，常常需要对信号进行预处理，而预处理最主要的一个步骤就是降噪。

     小波分析是近年来发展起来的一种新的信号处理工具，这种方法源于傅立叶分析，小波（wavelet），即小区域的波，仅仅在非常有限的一段区间有非零值，而不是像正弦波和余弦波那样无始无终。小波可以沿时间轴前后平移，也可按比例伸展和压缩以获取低频和高频小波，构造好的小波函数可以用于滤波或压缩信号，从而可以提取出已含噪声信号中的有用信号。

---

二、小波去噪的原理

Donoho提出的小波阀值去噪的基本思想是将信号通过小波变换（采用Mallat算法）后，信号产生的小波系数含有信号的重要信息，将信号经小波分解后小波系数较大，噪声的小波系数较小，并且噪声的小波系数要小于信号的小波系数，通过选取一个合适的阀值，大于阀值的小波系数被认为是有信号产生的，应予以保留，小于阀值的则认为是噪声产生的，置为零从而达到去噪的目的。

     从信号学的角度看 ,小波去噪是一个信号滤波的问题。尽管在很大程度上小波去噪可以看成是低通滤波 ,但由于在去噪后 ,还能成功地保留信号特征 ,所以在这一点上又优于传统的低通滤波器。由此可见 ,小波去噪实际上是特征提取和低通滤波的综合 ,其流程图如下所示：

     

      一个含噪的模型可以表示如下：

     

     其中 ,f( k)为有用信号,s(k)为含噪声信号,e(k)为噪声,ε为噪声系数的标准偏差。

     假设，e(k)为高斯白噪声,通常情况下有用信号表现为低频部分或是一些比较平稳的信号,而噪声信号则表现为高频的信号,我们对 s(k)信号进行小波分解的时候,则噪声部分通常包含在HL、LH、HH中,如下图所示，只要对HL、LH、HH作相应的小波系数处理,然后对信号进行重构即可以达到消噪的目的。

      

     我们可以看到，小波去噪的原理是比较简单类，类似以往我们常见的低通滤波器的方法，但是由于小波去找保留了特征提取的部分，所以性能上是优于传统的去噪方法的。

     

---

三、小波去噪的基本方法

     一般来说， 一维信号的降噪过程可以分为 3个步骤

      信号的小波分解。选择一个小波并确定一个小波分解的层次N，然后对信号进行N层小波分解计算。

      小波分解高频系数的阈值量化。对第1层到第N层的每一层高频系数（三个方向）， 选择一个阈值进行阈值量化处理．

     这一步是最关键的一步，主要体现在阈值的选择与量化处理的过程，在每层阈值的选择上matlab提供了很多自适应的方法， 这里不一一介绍，量化处理方法主要有硬阈值量化与软阈值量化。下图是二者的区别：

     

     上面左图是硬阈值量化，右图是软阈值量化。采用两种不同的方法，达到的效果是，硬阈值方法可以很好地保留信号边缘等局部特征，软阈值处理相对要平滑，但会造成边缘模糊等失真现象。   

      信号的小波重构。根据小波分解的第 N层的低频系数和经过量化处理后的第1层到第N 层的高频系数，进行信号的小波重构。

小波阀值去噪的基本问题包括三个方面：小波基的选择，阀值的选择，阀值函数的选择。
（1）小波基的选择：通常我们希望所选取的小波满足以下条件：正交性、高消失矩、紧支性、对称性或反对称性。但事实上具有上述性质的小波是不可能存在的，因为小波是对称或反对称的只有Haar小波，并且高消失矩与紧支性是一对矛盾，所以在应用的时候一般选取具有紧支的小波以及根据信号的特征来选取较为合适的小波。
（2）阀值的选择：直接影响去噪效果的一个重要因素就是阀值的选取，不同的阀值选取将有不同的去噪效果。目前主要有通用阀值（VisuShrink）、SureShrink阀值、Minimax阀值、BayesShrink阀值等。
（3）阀值函数的选择：阀值函数是修正小波系数的规则，不同的反之函数体现了不同的处理小波系数的策略。最常用的阀值函数有两种：一种是硬阀值函数，另一种是软阀值函数。还有一种介于软、硬阀值函数之间的Garrote函数。
另外，对于去噪效果好坏的评价，常用信号的信噪比（SNR）与估计信号同原始信号的均方根误差（RMSE）来判断。

参考：

小波阀值去噪法基础  http://blog.sina.com.cn/s/blog_4d7c97a00101cib3.html

在python中使用小波分析进行阈值去噪声,使用pywt.threshold函数

1.  
   #coding=gbk
2.  
   #使用小波分析进行阈值去噪声,使用pywt.threshold
3.  
    
4.  
   import pywt
5.  
   import numpy as np
6.  
   import pandas as pd
7.  
   import matplotlib.pyplot as plt
8.  
   import math
9.  
    
10.  
    data = np.linspace(1, 10, 10)
11.  
    print(data)
12.  
    # [ 1. 2. 3. 4. 5. 6. 7. 8. 9. 10.]
13.  
    # pywt.threshold(data, value, mode, substitute) mode 模式有4种，soft, hard, greater, less; substitute是替换值
14.  
     
15.  
    data_soft = pywt.threshold(data=data, value=6, mode='soft', substitute=12)
16.  
    print(data_soft)
17.  
    # [12. 12. 12. 12. 12. 0. 1. 2. 3. 4.] 将小于6 的值设置为12， 大于等于6 的值全部减去6
18.  
     
19.  
    data_hard = pywt.threshold(data=data, value=6, mode='hard', substitute=12)
20.  
    print(data_hard)
21.  
    # [12. 12. 12. 12. 12. 6. 7. 8. 9. 10.] 将小于6 的值设置为12， 其余的值不变
22.  
     
23.  
    data_greater = pywt.threshold(data, 6, 'greater', 12)
24.  
    print(data_greater)
25.  
    # [12. 12. 12. 12. 12. 6. 7. 8. 9. 10.] 将小于6 的值设置为12，大于等于阈值的值不变化
26.  
     
27.  
    data_less = pywt.threshold(data, 6, 'less', 12)
28.  
    print(data_less)
29.  
    # [ 1. 2. 3. 4. 5. 6. 12. 12. 12. 12.] 将大于6 的值设置为12， 小于等于阈值的值不变

1、小波变换的理解

傅里叶变换——短时傅里叶变换——小波变换。

参考文献：以下两篇参考资料讲述得十分清楚，有助于理解小波变换。

但具体的数学角度阐述，请参考其他资料。

（1）知乎专栏：形象易懂讲解算法I——小波变换

https://zhuanlan.zhihu.com/p/22450818

（2）知乎专栏：傅里叶分析之掐死教程。

https://zhuanlan.zhihu.com/p/19763358

2、小波包分解

小波包是为了克服小波分解在高频段的频率分辨率较差，而在低频段的时间分辨率较差的问题的基础上而提出的。

它是一种更精细的信号分析的方法，提高了信号的时域分辨率。

下面是两者的对比图：

3、能量谱

      基于小波包分解提取多尺度空间能量特征的原理是把不同分解尺度上的信号能量求解出来，将这些能量值按尺度顺序排列成特征向量供识别使用。

20180510补充更新：具体计算公式如下所示，本文中未使用重构后的系数进行能量值计算，直接使用小波包分解后的系数，参考文献《基于小波包能量特征的滚动轴承故障监测方法 》。

4、Matlab代码

给出两部分代码，写成两个函数。一个是小波包分解与重构，另一个是能量谱函数。

下载地址：https://download.csdn.net/download/ckzhb/10030651

代码名称：wavelet_packetdecomposition_reconstruct

1.  
   function wpt= wavelet_packetdecomposition_reconstruct( x,n,wpname )
2.  
   %% 对信号进行小波包分解，得到节点的小波包系数。然后对每个节点系数进行重构。 
3.  
   % Decompose x at depth n with wpname wavelet packets.using Shannon entropy.
4.  
   %   
5.  
   %  x-input signal,列向量。
6.  
   %  n-the number of decomposition layers
7.  
   %  wpname-a particular wavelet.type:string.
8.  
   %
9.  
   %Author hubery_zhang
10.  
    %Date 20170714
11.  
     
12.  
    %%
13.  
    wpt=wpdec(x,n,wpname);
14.  
    % Plot wavelet packet tree (binary tree)
15.  
    plot(wpt)
16.  
    %% wavelet packet coefficients.default：use the front 4.
17.  
    cfs0=wpcoef(wpt,[n 0]);
18.  
    cfs1=wpcoef(wpt,[n 1]);
19.  
    cfs2=wpcoef(wpt,[n 2]);
20.  
    cfs3=wpcoef(wpt,[n 3]);
21.  
    figure;
22.  
    subplot(5,1,1);
23.  
    plot(x);
24.  
    title('原始信号');
25.  
    subplot(5,1,2);
26.  
    plot(cfs0);
27.  
    title(['结点 ',num2str(n) '  1',' 系数'])
28.  
    subplot(5,1,3);
29.  
    plot(cfs1);
30.  
    title(['结点 ',num2str(n) '  2',' 系数'])
31.  
    subplot(5,1,4);
32.  
    plot(cfs2);
33.  
    title(['结点 ',num2str(n) '  3',' 系数'])
34.  
    subplot(5,1,5);
35.  
    plot(cfs3);
36.  
    title(['结点 ',num2str(n) '  4',' 系数'])
37.  
    %% reconstruct wavelet packet coefficients.
38.  
    rex0=wprcoef(wpt,[n 0]);
39.  
    rex1=wprcoef(wpt,[n 1]);
40.  
    rex2=wprcoef(wpt,[n 2]);
41.  
    rex3=wprcoef(wpt,[n 3]);
42.  
    figure;
43.  
    subplot(5,1,1);
44.  
    plot(x);
45.  
    title('原始信号');
46.  
    subplot(5,1,2);
47.  
    plot(rex0);
48.  
    title(['重构结点 ',num2str(n) '  1',' 系数'])
49.  
    subplot(5,1,3);
50.  
    plot(rex1);
51.  
    title(['重构结点 ',num2str(n) '  2',' 系数'])
52.  
    subplot(5,1,4);
53.  
    plot(rex2);
54.  
    title(['重构结点 ',num2str(n) '  3',' 系数'])
55.  
    subplot(5,1,5);
56.  
    plot(rex3);
57.  
    title(['重构结点 ',num2str(n) '  4',' 系数'])
58.  
    end

代码名称：wavelet_energy_spectrum

1.  
   function E = wavelet_energy_spectrum( wpt,n )
2.  
   %% 计算每一层每一个节点的能量
3.  
   %  wpt-wavelet packet tree
4.  
   %  n-第n层能量
5.  
   % 
6.  
   % Author hubery_zhang
7.  
   % Date  20170714
8.  
   %%
9.  
   % 求第n层第i个节点的系数
10.  
    E(1:2^n )=0;
11.  
    for i=1:2^n 
12.  
    E(i) = norm(wpcoef(wpt,[n,i-1]),2)^2; %20180604更新 原代码：E(i) = norm(wpcoef(wpt,[n,i-1]),2)
13.  
    end
14.  
    %求每个节点的概率
15.  
    E_total=sum(E); 
16.  
    for i=1:2^n
17.  
    p_node(i)= 100*E(i)/E_total;
18.  
    end
19.  
    % E = wenergy(wpt); only get the last layer
20.  
    figure;
21.  
    x=1:2^n;
22.  
    bar(x,p_node);
23.  
    title(['第',num2str(n),'层']);
24.  
    axis([0 2^n 0 100]);
25.  
    xlabel('结点');
26.  
    ylabel('能量百分比/%');
27.  
    for j=1:2^n
28.  
    text(x(j),p_node(i),num2str(p_node(j),'%0.2f'),...
29.  
        'HorizontalAlignment','center',...
30.  
        'VerticalAlignment','bottom') 

    end

    end

一维、二维离散卷积的计算方法：

一、  定义

离散信号f(n),g(n)的定义如下：

N-----为信号f(n)的长度

s(n)----为卷积结果序列,长度为len(f(n))+len(g(n))-1

以3个元素的信号为例：

f(n) = [1 2 3]; g(n) = [2 3 1];

s(0) = f(0)g(0-0) + f(1)g(0-1)+f(2)g(0-2) = 1*2 + 2*0 + 3*0 =2

s(1) = f(0)g(1-0) + f(1)g(1-1) + f(2)g(1-2) = 1*3 + 2*2 + 3*0 = 7

s(2) = f(0)g(2-0) + f(1)g(2-1) + f(2)g(2-2) =1*1 + 2*3 + 3*2=13

s(3) = f(0)g(3-0) + f(1)g(3-1) + f(2)g(3-2) =1*0 + 2*1 + 3*3=11

s(4) = f(0)g(4-0) + f(1)g(4-1) + f(2)g(4-2) =1*0 + 2*0 + 3*1=3

最终结果为:

     s(n) = [2 7 13 11 3]

上述计算图示如下：

在数学里我们知道f(-x)的图像是f(x)对y轴的反转

     g(-m)就是把g(m)的序列反转，g(n-m)的意义是把g(-m)平移的n点：

如上图g(m)在信号处理中通常叫做滤波器或掩码，卷积相当于掩码g(m)反转后在信号f(n)上平移求和。Matlab计算卷积的函数为conv,

>> A = [1 2 3];

B = [2,3,1];

convD = conv(A,B)

convD =

     2     7    13    11     3

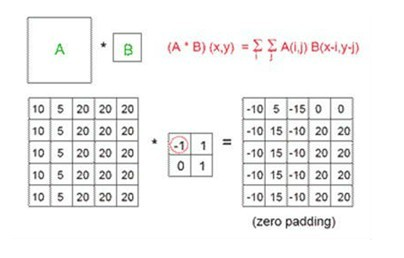
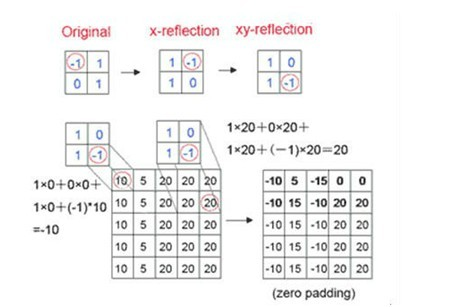
相应的二维卷积定义如下：