任何惊艳的偶然与巧合，都是自然的精妙计算与安排。
写在前面的话
作者在数字图像学习过程中，需要对图像进行空间域和频率域的转换，而傅里叶变换是进行空域（或时域）到频域变换的重要手段，因此对傅里叶变换做了深入研究。本文只是作者的学习心得，不适合作为学习材料，仅作交流之用。
傅里叶变换来源
傅里叶级数是高等数学的内容，傅里叶变换是傅里叶级数的发展。傅里叶级数是将复杂的周期函数用一系列简单的正余弦函数之和表示，而傅里叶变换则将非周期函数视作周期无穷大的周期函数求其“傅里叶级数”。
时域、空域、频域
我们生活的世界有两个重要的属性，一个是时间，另一个是空间。在时间域上我们看到了一个二维的世界，时间占了一个维度，另一个维度是世界的片段；在二维空间域上我们看到了一个三维的世界，二维空间占了两个维度，另一个维度是世界的片段。为什么要说这个，是因为图像处理是二维空间的处理，因此是空间域（其实是二维空间域）上的处理。与此相关联，音频的处理是时间域上的处理，而做三维物体分析的话则是三维空间上的处理，可以称之为三维空间域上的处理。
但是，这种在时域、空域上的处理，往往只是片面的。很多问题在频域中解决将会简单得多。比如滤波操作，在频域进行滤波就像加减法一样简单。
这也是本文题目的来源，傅里叶变换是从频率域角度看时间、空间，是一种新的世界观。
傅里叶级数
一语概之，傅里叶级数是将复杂的、周期性的连续函数分解为一系列简单的正余弦函数之和。那一系列正余弦函数构成的就是频率域，以正余弦函数的频率为横坐标，振幅为纵坐标得到的函数是频率域图像。
图1 傅里叶级数
（来自于Wikipedia）
图1表示的函数 s(x) （红色）是六个不同幅度的谐波关系的正弦函数的和。它们的和叫做傅里叶级数。傅里叶变换 S(f) （蓝色），针对幅度与频率进行描绘，显示出6种频率和它们的幅度。
傅里叶变换
如果说傅里叶级数是将周期性函数用振荡集合表示，那么傅里叶变换就是将非周期性函数用振荡集合表示。
频率谱、相位谱
傅里叶变换将复杂函数分解为振荡集合，确定振荡分量的要素有三：频率、振幅、相位。在频率谱中可以得到各个频率对应的振幅，在相位谱中则可以得到各个频率对应的相位。由此可以看出，傅里叶变换是沿着频率轴来寻找振荡分量的，每一种频率的振荡振幅和相位是多少，就是频率谱和相位谱。
欧拉公式
欧拉公式是复分析领域的公式，其物理意义是螺旋线。在实轴上的投影是余弦函数，在虚轴上的投影是正弦函数，二者叠加起来就是不断前进的圆周运动，构成了螺旋线。
为什么要提及欧拉公式？因为振荡的表示不仅可以用正余弦函数来表示，也可以用欧拉公式来表示（也即复数表示）。
上述两式分别表示两个方向相反的螺旋。
两种螺旋线叠加之后幅度减半，可以得到正余弦函数。
*之所以将欧拉公式称为最完美的公式，是因为当t=π时，欧拉公式变为
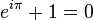e^(iπ) +1=0
在一个形式简单的公式中，有自然底数e、虚数i、圆周率常数π、自然数0和1。