原文参考:http://www.cnblogs.com/Anker/archive/2013/01/25/2876397.html
摘要:
本章先回顾了前面介绍的合并排序、堆排序和快速排序的特点及运行运行时间。合并排序和堆排序在最坏情况下达到O(nlgn),而快速排序最坏情况下达到O(n^2),平均情况下达到O(nlgn),因此合并排序和堆排序是渐进最优的。这些排序在执行过程中各元素的次序基于输入元素间的比较,称这种算法为比较排序。接下来介绍了用决策树的概念及如何用决策树确定排序算法时间的下界,最后讨论三种线性时间运行的算法:计数排序、基数排序和桶排序。这些算法在执行过程中不需要比较元素来确定排序的顺序,这些算法都是稳定的。
1、决策树模型
在比较排序算法中,用比较操作来确定输入序列<a1,a2,......,a3>的元素间次序。决策树是一棵完全二叉树,比较排序可以被抽象视为决策树,表示某排序算法作用域给定输入所做的比较。在决策树中,节点表示为i:j,其中1≤i,j≤n,n是待排序元素个数,叶子节点是排序的结果。节点的左子树满足ai≤aj,右子树满足ai>aj。排序算法正确工作的必要条件是:n个元素的n!中排列中的每一种都要作为决策树的一个叶子而出现。举例说明,先有序列A<3,2,1>,对其进行有小到达进行插入排序,排序的决策树如下图所示:
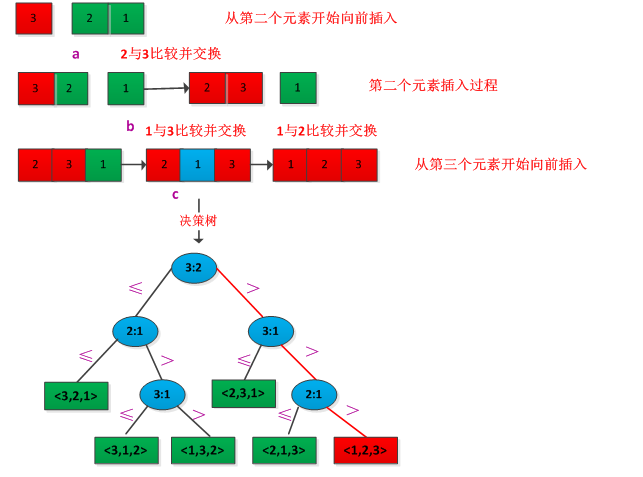
2、计数排序
计数排序假设n个输入元素中的每一个都介于0和k之间的整数,k为n个数中最大的元素。当k=O(n)时,计数排序的运行时间为θ(n)。计数排序的基本思想是:对n个输入元素中每一个元素x,统计出小于等于x的元素个数,根据x的个数可以确定x在输出数组中的最终位置。此过程需要引入两个辅助存放空间,存放结果的B[1...n],用于确定每个元素个数的数组C[0...k]。算法的具体步骤如下:
(1)根据输入数组A中元素的值确定k的值,并初始化C[1....k]= 0;
(2)遍历输入数组A中的元素,确定每个元素的出现的次数,并将A中第i个元素出现的次数存放在C[A[i]]中,然后C[i]=C[i]+C[i-1],在C中确定A中每个元素前面有多个元素;
(3)逆序遍历数组A中的元素,在C中查找A中出现的次数,并结果数组B中确定其位置,然后将其在C中对应的次数减少1。
举个例子说明其过程,假设输入数组A=<2,5,3,0,2,3,0,3>,计数排序过程如下: