《算法导论》读书笔记之第7章 快速排序

原文链接：http://www.cnblogs.com/Anker/archive/2013/01/24/2875234.html

本章介绍了快速排序及其算法分析，快速排序采用的是分治算法思想，对包含n个数的输入数组，最坏情况下运行时间为θ(n^2)，但是平均性能相当好，期望的运行时间为θ(nlgn)。另外快速排序能够就地排序（我理解是不需要引入额外的辅助空间，每次划分能确定一个元素的具体位置），在虚拟环境中能很好的工作。

1、快速排序的描述

　　快速排序算法采用的分治算法，因此对一个子数组A[p…r]进行快速排序的三个步骤为：

　　（1）分解：数组A[p...r]被划分为两个（可能为空）子数组A[p...q-1]和A[q+1...r]，给定一个枢轴，使得A[p...q-1]中的每个元素小于等于A[q]，A[q+1...r]中的每个元素大于等于A[q]，q下标是在划分过程中计算得出的。

　　（2）解决：通过递归调用快速排序，对子数组A[p...q-1]和A[q+1...r]进行排序。

　　（3）合并：因为两个子数组是就地排序，不需要合并操作，整个数组A[p…r]排序完成。

　　快速排序关键过程是对数组进行划分，划分过程需要选择一个主元素（pivot element）作为参照，围绕着这个主元素进划分子数组。举个列说明如何划分数组，现有子数组A={24，15，27，5，43，87，34}，以最后一个元素为主元素进行划分，划分过程如图所示：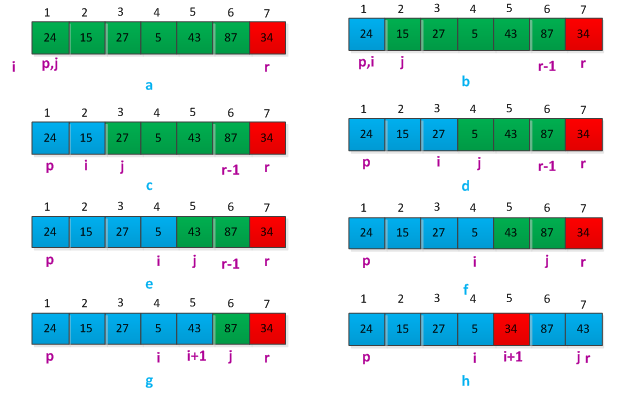

书中给出了划分过程的伪代码：

PARTITION(A,p,r)
   x = A[r]   //将最后一个元素作为主元素
  i = p-1
   for j=p to r-1     //从第一个元素开始到倒数第二个元素结束，比较确定主元的位置
        if A[j] <= x
             i = i+1
             exchange A[i] <-> A[j]
   exchange A[i+1]<->A[r]   //最终确定主元的位置
   return i+1   //返回主元的位置

根据划分过程的为代码，书中又给出了快速排序的伪代码：

 QUICKSORT(A,p,r)
2     if p<r
3        q = PARTITION(A,p,r)    //确定划分位置
4        QUICKSORT(A,p,q-1)     //子数组A[p...q-1]
5        QUICKSORT(Q,q+1,r)     //子数组A[q+1...r]

完整c++代码：

#include<iostream>
using namespace std;

void display (int a[], int n);
void swap (int& n, int& m);
int partition (int a[], int p, int r);
void quick_sort (int a[], int p, int r);

int main()
{
    int a[100];
    int n;
    while (cin >> n)
    {
        for (int i = 0; i < n; i++)
            cin >> a[i];
        quick_sort (a, 0, n - 1);
        display (a, n);
    }
    return 0;
}

void display (int a[], int n)
{
    for (int i = 0; i < n; i++)
        cout << a[i] << " ";
    cout << endl;
}

void swap (int& n, int& m)
{
    int temp;
    temp = n;
    n = m;
    m = temp;
}

int partition (int a[], int p, int r)
{
    int i = p - 1;
    for (int j = p; j < r; j++)
    {
        if (a[j] < a[r])
        {
            swap (a[++i], a[j]);
        }
    }
    swap (a[++i], a[r]);
    return i;
}

void quick_sort (int a[], int p, int r)
{
    if (p < r)
    {
        int q = partition (a, p, r);
        quick_sort (a, p, q - 1);
        quick_sort (a, q + 1, r);
    }
}

小甲鱼版c程序：逻辑不是很清晰 ， 建议不采用

#include<stdio.h>
void swap (int k[], int low, int high ) {
    int temp;
    temp = k[low];
    k[low] = k[high];
    k[high] = temp;
}
int Partition(int k[],int low, int high ) {

    int point;
    point = k[low];

    while(low< high) {
        while(low<high && k[high] >= point) {
            high--;
        }
        swap(k, low, high);

        while(low<high && k[low] <= point) {
            low++;
        }
        swap(k, low, high);
    }
    return low;

}

void QSort(int k[], int low , int high) {
    int point;

    if(low <high) {
        point = Partition(k ,low ,high);//calculate reference point

        QSort(k,low,point-1);
        QSort(k,point+1,high);
    }
}

void  QuickSort(int k[], int n){
    QSort(k, 0, n-1);
}
int main() {
    int i,a[10] = {5, 2, 6, 0, 3, 9, 1, 7, 4, 8};

    QuickSort(a,10);
    printf("the sorted result is: ");

    for (i=0; i<10; i++) {
        printf("%d", a[i]);
    }
    printf("
");

    return 0;
}