【JZOJ5231】【NOIP2017模拟A组模拟8.5】序列问题 线段树

题面

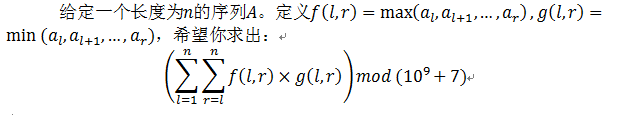
100

在(O(n^2))的基础上，我们可以用线段树来加速。
枚举了左端点之后，需要知道以这个左端点为起点的前缀max，前缀min。
这里只讨论前缀max，前缀min同理。
当我们倒序枚举左端点的时候，这个前缀max就可以用线段树来维护：
左端点向左移一位到i——
首先我们要预处理出a[i]向右第一个比他小的，以及第一个比他大的。
然后就相当于是区间赋值，并在线段树中维护好每一位的min和max积之和。
时间复杂度为(O(nlogn))。

code

#include<bits/stdc++.h>
#define ll long long
#define fo(i,x,y) for(int i=x;i<=y;i++)
#define fd(i,x,y) for(int i=x;i>=y;i--)
using namespace std;
const char* fin="seq.in";
const char* fout="seq.out";
const int inf=0x7fffffff;
int read(){
	int x=0;
	char ch=getchar();
	while (ch<'0' || ch>'9') ch=getchar();
	while (ch>='0' && ch<='9') x=x*10+ch-'0',ch=getchar();
	return x;
}
const int maxn=500007,mo=1000000007;
int n,a[maxn],ans,mx[maxn],mn[maxn],st[maxn];
struct node{int x,a,b,ma,mb;node(){ma=mb=-1;}}c[maxn*4];
void mkd(int l,int r,int t){
	if (c[t].ma!=-1){
		c[t].x=1ll*c[t].b*c[t].ma%mo;
		c[t].a=1ll*c[t].ma*(r-l+1)%mo;
		if (l<r){
			c[t*2].ma=c[t].ma;
			c[t*2+1].ma=c[t].ma;
		}
		c[t].ma=-1;
	}
	if (c[t].mb!=-1){
		c[t].x=1ll*c[t].a*c[t].mb%mo;
		c[t].b=1ll*c[t].mb*(r-l+1)%mo;
		if (l<r){
			c[t*2].mb=c[t].mb;
			c[t*2+1].mb=c[t].mb;
		}
		c[t].mb=-1;
	}
}
void modifya(int l,int r,int t,int v1,int v2,int v){
	int mid=(l+r)/2;
	mkd(l,r,t);
	if (l>v2 || r<v1) return;
	if (l>=v1 && r<=v2){
		c[t].ma=v;
		mkd(l,r,t);
		return;
	}
	modifya(l,mid,t*2,v1,v2,v);
	modifya(mid+1,r,t*2+1,v1,v2,v);
	c[t].x=(c[t*2].x+c[t*2+1].x)%mo;
	c[t].a=(c[t*2].a+c[t*2+1].a)%mo;
	c[t].b=(c[t*2].b+c[t*2+1].b)%mo;
}
void modifyb(int l,int r,int t,int v1,int v2,int v){
	int mid=(l+r)/2;
	mkd(l,r,t);
	if (l>v2 || r<v1) return;
	if (l>=v1 && r<=v2){
		c[t].mb=v;
		mkd(l,r,t);
		return;
	}
	modifyb(l,mid,t*2,v1,v2,v);
	modifyb(mid+1,r,t*2+1,v1,v2,v);
	c[t].x=(c[t*2].x+c[t*2+1].x)%mo;
	c[t].a=(c[t*2].a+c[t*2+1].a)%mo;
	c[t].b=(c[t*2].b+c[t*2+1].b)%mo;
}
int main(){
	freopen(fin,"r",stdin);
	freopen(fout,"w",stdout);
	n=read();
	fo(i,1,n) a[i]=read();
	st[0]=0;
	fd(i,n,1){
		while (st[0] && a[st[st[0]]]>=a[i]) st[0]--;
		if (!st[0]) mx[i]=n+1;
		else mx[i]=st[st[0]];
		st[++st[0]]=i;
	}
	st[0]=0;
	fd(i,n,1){
		while (st[0] && a[st[st[0]]]<=a[i]) st[0]--;
		if (!st[0]) mn[i]=n+1;
		else mn[i]=st[st[0]];
		st[++st[0]]=i;
	}
	fd(i,n,1){
		modifya(1,n,1,i,mx[i]-1,a[i]);
		modifyb(1,n,1,i,mn[i]-1,a[i]);
		ans=(ans+c[1].x)%mo;
	}
	printf("%d",ans);
	return 0;
}