这篇博文主要讲解下梯度与方向导数的关系、等值线图中梯度的表示，以及梯度的应用。因涉及太多高数的知识点，在此就不一一详述了，只是简单梳理下知识点，有所纰漏还望纠正指出，文末附有参考文献，借图。
一、方向导数与梯度
1、方向导数
- 导数引言
我们知道在二维平面上，F(x,y)=0 有斜率的概念，从名字上看就是“倾斜的程度” 。百度百科的解释：表示一条直线(或曲线的切线)关于(横)坐标轴倾斜程度的量。它通常是直线(或曲线的切线)与(横)坐标轴夹角的正切，或两点的纵坐标之差与横坐标之差的比来表示。导数的几何意义就是该函数曲线在这一点上的切线斜率，曲线上的点可导时，也就能找到过该点的切线。
- 方向导数
知道了二维平面上的斜率（即导数）的概念，延伸到三维呢？那就有了方向导数的概念，在二维平面上，任何曲线上可导一点都能找到切线，那曲面上有全微分（可微）的一点都能找到过该点的一个切平面，并且在切平面上任意方向的向量都是该点的方向导数。下面形式化表述什么是全微分，以及方向导数怎么定义。
- 形式化表述
我们先了解下全增量的概念：
如果函数 z=f(x,y) 在点p(x,y) 的某邻域内有定义，设为这邻域内任意一点，则称这两点的函数值之差 
为函数在点p对应于自变量增量的全增量，记为
。
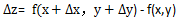全微分：
若在p点的全增量 Δz 可以表示为 Δz=AΔx+BΔy+o(ρ)，其中A、B不依赖于Δx, Δy，仅与x,y有关，ρ趋近于0，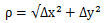
，此时称函数z =f(x, y)在点 p 处可微分，AΔx+BΔy 称为函数z=f(x, y)在点(x, y)处的全微分，记为 dz=AΔx +BΔy。那么A、B分别怎么求呢？该函数在点(x,y)的偏导数 
，当Δx=0 和 Δy分别为0 时，利用全增量的公式可推出，
。
我们上面提到了偏导数的概念，下面给出偏导数几何意义：
做了这么多铺垫，终于到了主角方向导数出场了。
我们对比二维平面上曲线的导数来理解方向导数的概念，导数的公式是
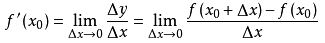
三维空间的方向导数公式如下：
其中ρ趋近于0，
由以上求得全微分的公式 ，代入即
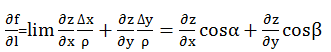其中ρ趋近于0，（见下图）
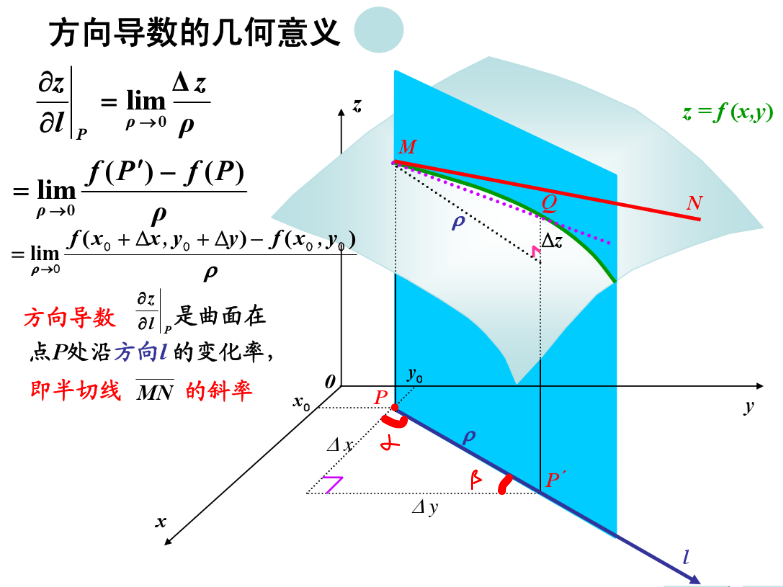
2、梯度
- 梯度的由来
函数 z = f(x,y) 在p(x,y) 点沿哪一方向增加的速度最快? 我们定义梯度的方向是函数在该点增长最快的方向。由方向导数公式推导如下
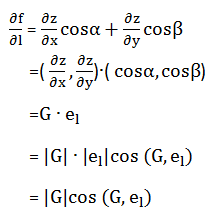其中cos(G,el)=1时，方向导数取得最大值 |G|，我们称G为梯度。梯度的方向与偏导的方向一致，增加的速度最快。二元函数z=f(x,y)的梯度，记为
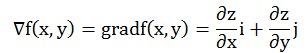
可知，函数在某点的梯度是一个向量，它是方向导数取得最大值的方向，而它的模为方向导数的最大值。
- 等值线与梯度的表示
梯度的方向与过点p的等值线上的法向量的一个方向相同，且指向等值线（函数值）增加的方向。在几何上 z = f(x,y) 表示一个曲面，曲面被 z=c 所截得的曲线在xoy轴投影如下图2，对f(x,y) = c2 对x求导，其中涉及到y是x的隐变量，得
在p点的切线斜率是
，则由以上公式可得法向量的斜率是
，这也正是梯度的斜率（下图1）。又由于沿梯度的方向导数大于0，所以沿梯度方向是函数增加。
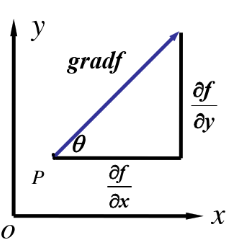
图1
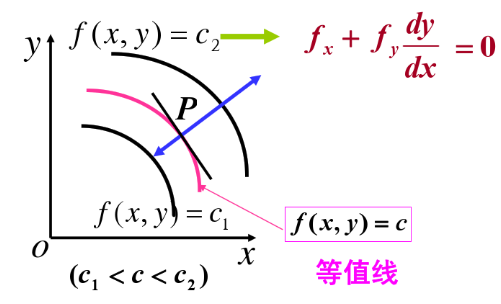
图2
二、梯度的应用
在机器学习领域，梯度有很广泛的应用，比如常见的梯度下降算法，它是求解无约束最优化问题的一种常用方法。我们先列出损失函数，求损失函数的最小，我们只要沿着梯度的反方向下降，一步步到极小值。这也是一种贪心算法。但是在求梯度的时候，往往要用到全部训练样本，当训练样本数量大的时候，这是个很耗时的工程，所以提出随机梯度下降和批量梯度下降，求解梯度选用少量样本。
参考博客：
高数同济9.7方向导数和梯度 https://wenku.baidu.com/view/fba284f0172ded630b1cb685.html
第6章多元函数微分学3-10(全增量及全微分) https://wenku.baidu.com/view/4f39fda0941ea76e59fa041d.html