Kruskal算法

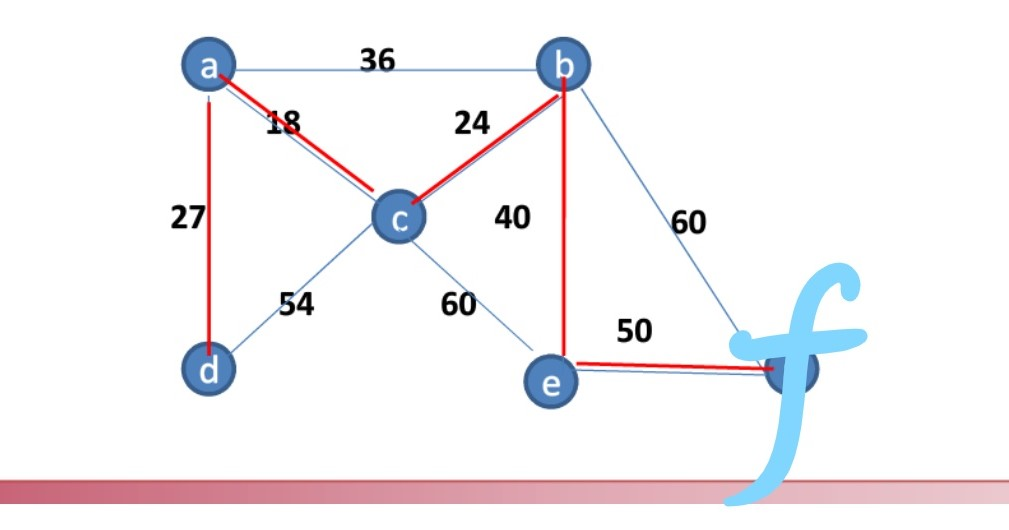
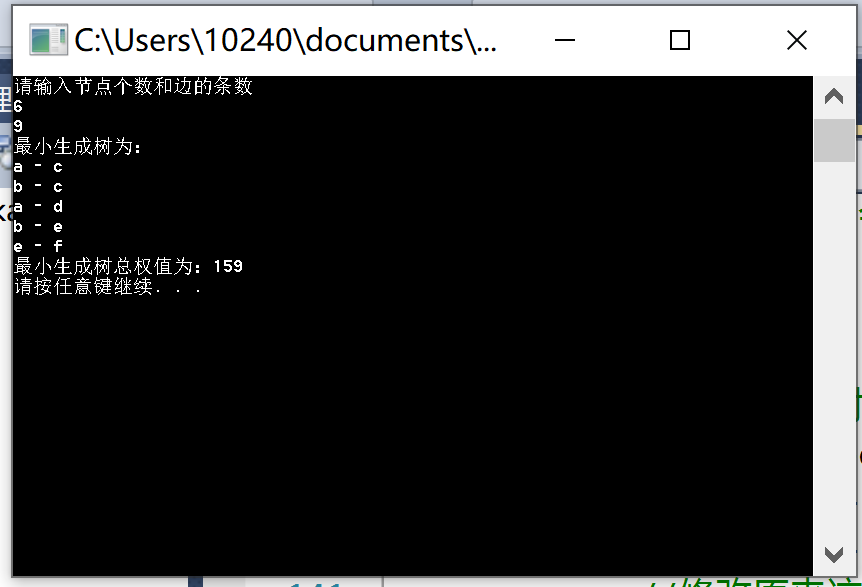
思路有参考：

http://data.biancheng.net/view/41.html

思路；

源代码见: https://github.com/nxkjwbxewudh/Kruskal

edge[MAX]保存所有的边，每条边存储起始结点、终止结点和权重；

先把所有边按照升序排序，这里用到了sort，需要#include<algorithm> ；

从edge[MAX]里（就是排序后的数组）以此取出一条边，首先判断这条边能不能加入最小生成树（记得另外定义一个变量minTree[MAX]保存结果）；

   判断方法：

   新建一个辅助数组，保存所有顶点，一开始，每个顶点都有一个独一无二的set值，用来表示他们的终点；

   因为形成回路的条件就是取出来的当前这条边的两个顶点的终点相同，也就是set值相同；

   所以每次取出一条边，就要判断是否两顶点set值相等；

   不相等的话就可以添加到最小生成树中。每次添加了一个新的边就要修改一个顶点的set值；

#include<iostream>
#include<algorithm>     //为了使用sort函数对所有边按照权重进行升序排序
#include<stdlib.h>
#include<string>
#include<fstream>
using namespace std;

#define MAX 100
struct node{
   char startNode;
   char endNode;
   int  weight;
}edge[MAX]={
    {'a','b',36},
    {'a','c',18},
    {'a','d',27},
    {'c','d',54},
    {'c','e',60},
    {'b','e',40},
    {'e','f',50},
    {'b','f',60},
    {'b','c',24}
};
struct helpGroup
{
   char nodeName;
   int  rootNodeSet;      //如果选择的这条边的顶点的终点结点是同一个set，那么就会形成回路   
}assistGroup[MAX]={
    {'a',1},
    {'b',2},
    {'c',3},
    {'d',4},
    {'e',5},
    {'f',6}
};

/**
 * 用于打印结果
 * 输入：minTree边的条数和minTree数组
 * 输出：打印每条边，形式为start-end,并且返回总权值，函数返回类型void
 * **/
void printMyTree(int n, node given[], int sum){
   int i = 0;
   cout<<"最小生成树为："<<endl;
   for(i=0;i<n;i++){
      cout<<given[i].startNode<<" - "<<given[i].endNode<<endl;
   }
   cout<<"最小生成树总权值为："<<sum<<endl;
}

/**
 * 用于判断是否会形成回路
 * 输入：n,一条边的初始/末尾结点
 * 输出：这个节点在辅助数组中的位置,函数返回类型int
 * **/
int getNodePlace(int n, char nodeName){
    int i=0;
    for(i=0;i<n;i++){
       if(assistGroup[i].nodeName == nodeName){
          return i;
       }
    }
    return -1;
}

/**
 * 修改当前这条边上的某一个结点的set值
 * 遍历辅助数组，遇到set值和某个结点set值相等的话，就更新另一个结点的set
 * 如果这两个节点都不在当前的树中，就把终点结点的set赋值给起始节点的set
 * 输入：n,init,end
 * 输出：只是修改，函数返回类型void
 * **/
void changeSet(int n, int start, int end){
   int i=0;
   for(i=0;i<n;i++){
      if(assistGroup[start].rootNodeSet == assistGroup[i].rootNodeSet){
         assistGroup[end].rootNodeSet = assistGroup[start].rootNodeSet;
         break;
      }
      if(assistGroup[end].rootNodeSet == assistGroup[i].rootNodeSet){
         assistGroup[start].rootNodeSet = assistGroup[end].rootNodeSet;
         break;
      }
   }
   assistGroup[start].rootNodeSet = assistGroup[end].rootNodeSet;
}

bool cpm(node x, node y){
   if(x.weight==y.weight){
      return x.startNode<y.startNode;
   }
   else{
      return x.weight<y.weight;
   }
}

int main(){
   int sum=0;                            //总权值
   int nodeNum=0;
   int edgeNum=0;      
   cout<<"请输入节点个数和边的条数"<<endl;
   cin>>nodeNum>>edgeNum;              //获得顶点数目和边数
   int n=edgeNum;                      //n代表边数
   
 /*初始化最小生成树，所有边按权值排序*/
   int treeCount=0;                    //最小生成树结点个数
   node minTree[MAX];                  //用于保存结果最小生成树
   sort(edge,edge+n,cpm);              //将所有边按照权值升序排序，并取代edge数组
   //int k=0;
   /*cout<<"edge升序排序之后的结果"<<endl;
   for(k=0;k<n;k++){
       cout<<edge[k].startNode<<"->"<<edge[k].endNode<<endl;
   }
   */

 /*从edge里选一条边，如果这条边的两个顶点的set值相等，表示会形成回路*/
   int i=0;
   int init=0;
   int end=0;
   int initSet=0;
   int endSet=0;
   for(i=0;i<n;i++){
      init = getNodePlace(nodeNum, edge[i].startNode) ;
      end  = getNodePlace(nodeNum, edge[i].endNode) ;
      initSet = assistGroup[init].rootNodeSet;
      endSet = assistGroup[end].rootNodeSet;
      if((init==-1)||(end==-1)){
         cout<<"程序出错，应该是初始化问题"<<endl;
      }
      else
      {
         if(initSet==endSet){
            continue;//会形成回路
         }
         else
         {
            //可以加入树中
            minTree[treeCount] = edge[i];
            treeCount++;
            sum = sum + edge[i].weight;
            //修改原来这条边上结点的set值，使之等于当前最新的树上的set值
            changeSet(edgeNum,init,end);    
            if(treeCount == (nodeNum-1)){
               break;
            }
         }
         
      }
      
   }//end_of_big_loop

   printMyTree(treeCount,minTree,sum);
   system("pause");
   return 0;
}

 源代码见: https://github.com/nxkjwbxewudh/Kruskal