Description
FGD想从成都去上海旅游。在旅途中他希望经过一些城市并在那里欣赏风景,品尝风味小吃或者做其他的有趣的事情。经过这些城市的顺序不是完全随意的,比如说FGD不希望在刚吃过一顿大餐之后立刻去下一个城市登山,而是希望去另外什么地方喝下午茶。幸运的是,FGD的旅程不是既定的,他可以在某些旅行方案之间进行选择。由于FGD非常讨厌乘车的颠簸,他希望在满足他的要求的情况下,旅行的距离尽量短,这样他就有足够的精力来欣赏风景或者是泡MM了_.整个城市交通网络包含N个城市以及城市与城市之间的双向道路M条。城市自1至N依次编号,道路亦然。没有从某个城市直接到它自己的道路,两个城市之间最多只有一条道路直接相连,但可以有多条连接两个城市的路径。任意两条道路如果相遇,则相遇点也必然是这N个城市之一,在中途,由于修建了立交桥和下穿隧道,道路是不会相交的。每条道路都有一个固定长度。在中途,FGD想要经过K(K<=N-2)个城市。成都编号为1,上海编号为N,而FGD想要经过的N个城市编号依次为2,3,…,K+1.举例来说,假设交通网络如下图。FGD想要经过城市2,3,4,5,并且在2停留的时候在3之前,而在4,5停留的时候在3之后。那么最短的旅行方案是1-2-4-3-4-5-8,总长度为19。注意FGD为从城市2到城市4可以路过城市3,但不在城市3停留。这样就不违反FGD的要求了。并且由于FGD想要走最短的路径,因此这个方案正是FGD需要的。
Input
第一行包含3个整数N(2<=N<=20000),M(1<=M<=200000),K(0<=K<=20),意义如上所述。
Output
只包含一行,包含一个整数,表示最短的旅行距离。
Sample Input
8 15 4
1 2 3
1 3 4
1 4 4
1 6 2
1 7 3
2 3 6
2 4 2
2 5 2
3 4 3
3 6 3
3 8 6
4 5 2
4 8 6
5 7 4
5 8 6
3
2 3
3 4
3 5
Sample Output
19
Hint
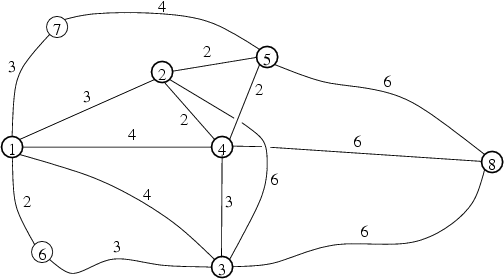
上面对应于题目中给出的例子。
题解
一道典型的状压(DP),先跑一边(Dijkstra),再状压一下
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<string>
#include<algorithm>
#include<cmath>
#include<queue>
#include<stack>
#include<set>
#include<map>
#include<bitset>
#include<vector>
#include<iomanip>
using namespace std;
const int N=25000,M=500000,K=35;
int n,m,k,pr[K],dp[1100000][K];
struct edge
{
int v,w,nx;
}e[M];
int ne,hd[N],p1[K],p2[K];
void Build(int u,int v,int w)
{
++ne,e[ne]=(edge){v,w,hd[u]},hd[u]=ne;
}
void Read()
{
scanf("%d%d%d",&n,&m,&k);
int u,v,w;
for(int i=1;i<=m;++i)
{
scanf("%d%d%d",&u,&v,&w),
--u,--v,
Build(u,v,w),
Build(v,u,w);
}
}
const int INF=0x3F3F3F3F;
typedef pair<int,int> pa;
priority_queue<pa,vector<pa>,greater<pa> > Q;
int v[N],d[K][N];
void Dijkstra(int s)
{
for(int i=0;i<=n;++i)
d[s][i]=INF,v[i]=0;
d[s][s]=0;
Q.push(make_pair(0,s));
int tp;
while(!Q.empty())
{
tp=Q.top().second; Q.pop();
if(v[tp]) continue;
v[tp]=1;
for(int i=hd[tp];i;i=e[i].nx)
if(d[s][e[i].v]>d[s][tp]+e[i].w)
{
d[s][e[i].v]=d[s][tp]+e[i].w;
Q.push(make_pair(d[s][e[i].v],e[i].v));
}
}
}
void Bit_DP()
{
for(int i=0;i<=(1<<k);++i)
for(int j=0;j<=k;++j) dp[i][j]=INF;
for(int i=1;i<=k;++i)
if(!pr[i]) dp[1<<(i-1)][i]=d[i][0];
int n1,n2,x,y;
for(int i=0;i<(1<<k);++i)
{
n1=n2=0;
for(int j=1;j<=k;++j)
if(i&(1<<(j-1))) ++n1,p1[n1]=j;
else ++n2,p2[n2]=j;
for(int j=1;j<=n1;++j)
for(int z=1;z<=n2;++z)
{
x=p1[j],y=p2[z];
if((i&pr[y])!=pr[y]) continue;//还不能去
dp[i+(1<<(y-1))][y]=min(
dp[i+(1<<(y-1))][y],
dp[i][x]+d[x][y]);
}
}
int Ans=INF;
for(int i=1;i<=k;++i)
Ans=min(Ans,dp[(1<<k)-1][i]+d[i][n-1]);
printf("%d
",Ans);
}
int main()
{
Read();
for(int i=0;i<=k;++i) Dijkstra(i);
if(k==0) {printf("%d
",d[0][n-1]);goto end;}
int x,y,kk;
scanf("%d",&kk);
for(int i=1;i<=kk;++i)
{
scanf("%d%d",&x,&y),
--x,--y,
pr[y]|=1<<(x-1);
}
Bit_DP();
end:
return 0;
}