最大的子序列和的问题：

题目链接：https://pintia.cn/problem-sets/434/problems/5404

法一：

int MaxSubseqSum1(int List[], int N)
{
    int i, j, k;
    int ThisSum, MaxSum = 0;
    for (i = 0; i < N; i++)
    {
        for (j = i; j < N; j++)
        {
            ThisSum = 0;                //ThisSum是从List[i]到List[j]的子列和
        
            for (k = i; k <= j; k++)
                ThisSum += List[k];
            if (ThisSum > MaxSum)
                MaxSum = ThisSum;
        }
        
    }
    return MaxSum;
}

这个算法的算法复杂度是O(N^3),是个非常差劲的算法，在pat提交时，提示时间超时，下面是提交结果

法二：

int MaxSubseqSum2(int List[], int N)
{
    int i, j;
    int ThisSum, MaxSum = 0;
    for (i = 0; i < N; i++)
    {
        ThisSum = 0;                //ThisSum是从List[i]到List[j]的子列和
        for (j = i; j < N; j++)
        {
            ThisSum += List[j];
            if (ThisSum > MaxSum)
                MaxSum = ThisSum;
        }
    }
    return MaxSum;
}

在法一的基础上进行了改进，将算法复杂度降到了O(N^2),已经比算法一好了很多倍，但是，优秀的程序员在看到一个算法的复杂度是O(N^2)时，都会尝试能不能将它降到O(NlogN）,下面是算法二的提交结果

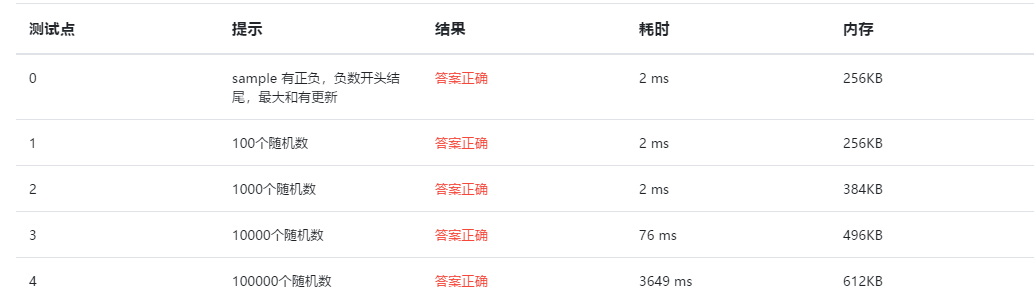
可以看出当测试数据增加到10^6个数量级时，算法是要花费大量时间的。

法三：

int Max3(int A, int B, int C)
{
    return A > B ? (A > C ? A : C) : (B > C ? B : C);

}

利用分治思想

int MaxSum(int List[], int Left, int Right)
{
    int MaxLeftSum, MaxRightSum;
    int MaxLeftBorderSum, MaxRightBorderSum;    //存放跨越分界线的结果
    int LeftBorderSum, RightBorderSum;

    int center, i;
    if (Left == Right)
    {
        if (List[Left] > 0) return List[Left];
        else
            return 0;
    }
    center = (Left + Right) / 2;
    MaxLeftSum = MaxSum(List, Left, center);
    MaxRightSum = MaxSum(List, center + 1, Right);
    LeftBorderSum = 0, MaxLeftBorderSum = 0;
    for (i = center; i >= Left; i--)
    {
        LeftBorderSum += List[i];
        if (LeftBorderSum > MaxLeftBorderSum)
            MaxLeftBorderSum = LeftBorderSum;
    }

    RightBorderSum = 0; MaxRightBorderSum = 0;
    for (i = center + 1; i <= Right; i++)
    {
        RightBorderSum += List[i];
        if (RightBorderSum > MaxRightBorderSum)
            MaxRightBorderSum = RightBorderSum;
    }

    //下面返回治的结果
    return Max3(MaxLeftSum, MaxRightSum, MaxLeftBorderSum + MaxRightBorderSum);
}

为了和其他算法统一接口，封装一下这个算法，让它和上面两个算法有相同的参数列表接口

int MaxSubseqSum3(int List[], int n)
{
    return MaxSum(List, 0, n - 1);
}

这个算法的复杂度是O(NlogN)，在上一个算法的性能上又进行了极大的优化，下面是提交结果：

可以看到，但测试数据很大时，算法花费的时间得到了极大的缩减，可以说是一个性能的极大飞跃，但是，还有一个牛到爆炸的算法，不仅算法简短，而且它的算法复杂度是O(N).。这就是传说中的法四

法四：

int MaxSubseqSum4(int List[], int n)
{
    int i, ThisSum = 0, MaxSum = 0;
    for (i = 0; i < n; i++)
    {
        ThisSum += List[i];
        if (ThisSum > MaxSum)
            MaxSum = ThisSum;
        else
        if (ThisSum < 0)
            ThisSum = 0;
    }

    return MaxSum;
}

下面是pat提交结果：

虽然从运行时间上看来，这个算法和上一个算法的相差不大（这是因为O(NlogN）本就是一个非常高效的算法了，所以在测试数据不是很大的情况下，性能上的差距可能不明显，但是如果进一步增大测试数据的数量级，还是能看到性能上的差距的