剑指 Offer 68 - II. 二叉树的最近公共祖先 & 236. 二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
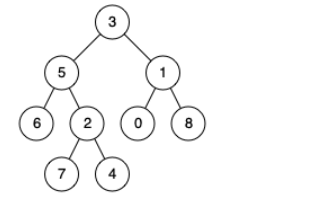
示例 1:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。
示例 2:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 输出: 5 解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身
说明:
所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉树中。
解法:
设root为最近公共祖先,那么p 和 q的分布有三种情况,分别是:
1. p和q分别在在root的左右子树上
2. p == root
3. q == root
算法的具体实现如下
1. 如果root为空,那么直接返回空
2. 如果p和q等于root, 那么最近公共祖先就是p或q即root
3. 否则遍历左子树,在左子树中寻找p或q的公共祖先,left
4. 遍历右子树,在右子树中寻找p或q的公共祖先,right
5. 如果left为空,说明左子树没有p或者q, 也就没有公共祖先,那说明q和p都在右子树,所以q和p的公共祖先就是right, 同理right为空;如果left和right都不为空,说明q 和 p分布在不同的子树上,root是他们的最近公共祖先
1 class Solution { 2 public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) { 3 4 // 1. 如果root为空,那么直接返回空 5 if(root == null) 6 return null; 7 // 2. 如果p和q等于root, 那么最近公共祖先就是p或q即root 8 if(p == root || q == root) 9 return root; 10 // 3. 否则遍历左子树,找到p或q的公共祖先,left 11 TreeNode left = lowestCommonAncestor(root.left, p, q); 12 // 4. 遍历右子树,找到p或q的公共祖先,right 13 TreeNode right = lowestCommonAncestor(root.right, p, q); 14 // 5. 如果left为空,说明左子树没有p或者q, 也就没有公共祖先,那说明q和p都在右子树, 15 // 所以q和p的公共祖先就是right, 同理right为空 16 if(left == null) 17 return right; 18 else if(right == null) 19 return left; 20 else 21 return root; // 如果left和right都不为空,说明q 和 p分布在不同的子树上,root是他们的最近公共祖先 22 } 23 }
leetcode运行时间为:9ms, 空间为:41.2MB
复杂度分析:
时间复杂度:相当于遍历整棵树寻找 p 和 q 两个结点,所以时间复杂度为 O(n)
空间复杂度:空间复杂度取决于栈的深度,栈的最大深度为树的高度,所以平均空间复杂度为O(logn)