94. 二叉树的中序遍历
给定一个二叉树,返回它的中序 遍历。
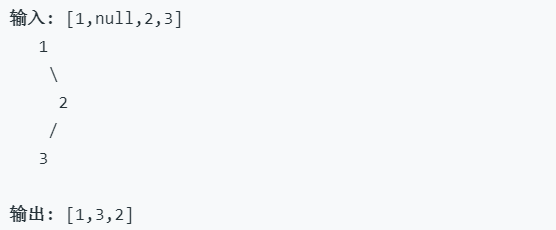
示例:
思路一:递归写法
定义一个列表,加入左子树的所有结点值,加入根节点值,加入右子树的值
1 // 递归写法 2 class Solution { 3 public List<Integer> inorderTraversal(TreeNode root) { 4 List<Integer> list = new ArrayList<Integer>(); 5 if(root != null){ 6 list.addAll(inorderTraversal(root.left)); 7 list.add(root.val); 8 list.addAll(inorderTraversal(root.right)); 9 } 10 return list; 11 } 12 }
力扣测试时间为:1ms, 空间为:38.5mb
复杂度分析:
时间复杂度为O(n)
思路一的另一种写法:
下面这种递归下方效率更高:
1 class Solution { 2 public List<Integer> inorderTraversal(TreeNode root) { 3 List<Integer> res = new ArrayList<Integer>(); 4 if(root != null){ 5 helper(root, res); 6 } 7 return res; 8 } 9 10 public void helper(TreeNode root, List<Integer> res){ 11 if(root != null){ 12 helper(root.left, res); 13 res.add(root.val); 14 helper(root.right, res); 15 } 16 } 17 }
力扣测试时间为:0ms, 空间为38.3mb
复杂度分析:
时间复杂度为O(n)
空间复杂度为O(n),每个结点的结点值都加入了列表一次,如果忽略这个的话,那么栈的递归层次最大为O(n), 平均为O(logn)
思路二:迭代写法
1 // 迭代写法 2 class Solution { 3 public List<Integer> inorderTraversal(TreeNode root) { 4 List<Integer> list = new ArrayList<Integer>(); 5 // 借助一个栈 6 Stack<TreeNode> stack = new Stack<>(); 7 TreeNode top = root; 8 while(!stack.isEmpty() || top != null){ 9 // 碰到一个结点就不停的向左移动 10 while(top != null){ 11 stack.push(top); 12 top = top.left; 13 } 14 top = stack.pop(); 15 // 访问这个结点 16 list.add(top.val); 17 18 // 指向右结点 19 top = top.right; 20 } 21 return list; 22 } 23 }
力扣测试时间为1ms,空间为38mb
复杂度分析:
时间复杂度为:将每个结点都访问了一遍,并且都入栈了一次,所以时间复杂度为O(n)
空间复杂度:空间的主要取决于栈的大小,栈的大小就是树的高度,所以最坏情况下空间复杂度为O(n), 最好情况下为O(logn)