剑指offer 6.旋转数组的最小数字 & 剑指 Offer 11. 旋转数组的最小数字

剑指 Offer 11. 旋转数组的最小数字

6. 旋转数组的最小数字

题目描述

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。
输入一个非递减排序的数组的一个旋转，输出旋转数组的最小元素。
例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转，该数组的最小值为1。
NOTE：给出的所有元素都大于0，若数组大小为0，请返回0。

法一：

暴力搜索, 遍历数组，后一个数字比前一个数字小的就是那个最小的数字, 如果遍历数组没找到这样的数字，说明所有元素都相等，直接返回numbers[0]

class Solution {
    public int minArray(int[] numbers) {
         // 遍历数组，后一个数字比前一个数字小的就是那个最小的数字
         int len = numbers.length;
         for(int i = 0; i < len - 1; i++){
             if(numbers[i] > numbers[i+1]){
                 return numbers[i+1];
             }
         }
         // 如果遍历数组没找到这样的数字，说明所有元素都相等，直接返回numbers[0]
         return numbers[0];
    }
}

leetcode运行时间为

复杂度分析：

时间复杂度：最坏情况下需要遍历整个数组，所以时间复杂度为O(n)

空间复杂度：O(1)

法二：

利用二分法的变形

分析：二分查找变种，没有具体的值用来比较。那么用中间值和高低位进行比较，看处于递增还是递减序列，进行操作缩小范围。

1. 处于递增：low上移

2. 处于递减：high下移（如果是high-1，则可能会错过最小值，因为找的就是最小值）

3. 其余情况：low++缩小范围

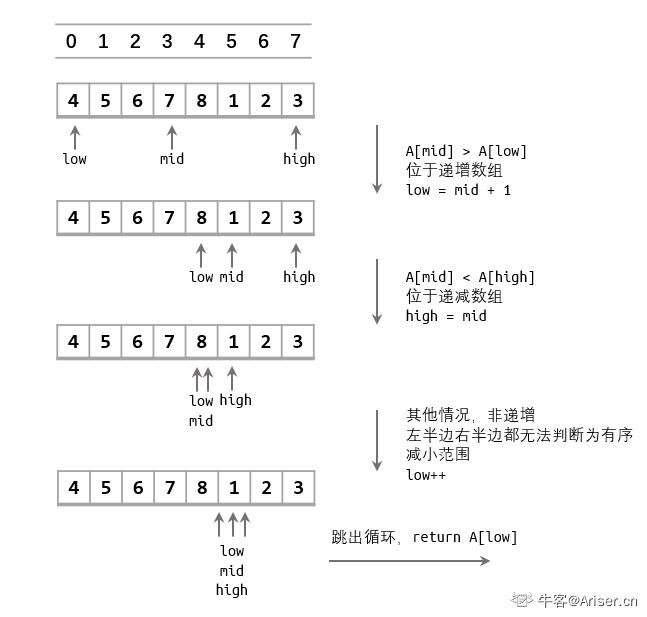
特殊情况：

import java.util.ArrayList;
public class Solution {
    public int minNumberInRotateArray(int [] array) {
        // 从头到尾扫描，记录前一个值大于后一个值的位置
        if(array.length <= 0)
            return 0;
        // 变形的二分查找
        int low = 0, high = array.length - 1;
        int mid;
        while(low < high){
            mid = (high - low) / 2 + low;
            if(array[low] < array[high])
                return array[low];
            if(array[mid] > array[low]){
                low = mid + 1;
            }else if(array[mid] < array[high]){
                high = mid;
            }else{
                low++;
            }
        }
       return array[low];
    }
}

思路三

这个方法其实和思路二一样，只不过这里是让array[mid]与array[high]比较，如果array[mid] < array[high]， 说明mid在右半段有序数组中，那应该high = mid; 如果array[mid] > array[high]，说明mid在左半段有序数组中，执行low = mid + 1, 如果array[mid] == array[high]，无法确定mid在哪个有序数组中，执行hight--来缩小范围。

class Solution {
    public int minArray(int[] numbers) {
         // 二分法
         int left = 0, right = numbers.length-1;
         int mid = 0;
         while(left < right){
             mid = (right + left) / 2;
            if(numbers[mid] > numbers[right]){  // 说明mid在左半段，旋转点在它后面
                left = mid + 1;
            }else if(numbers[mid] < numbers[right]){    // 说明mid在右半段，mid可能刚好是旋转点也可能旋转点在mid左侧
                right = mid;
            }else{
                right--;        // 无法确定mid的位置，也无法确定旋转点的位置
            }
         }
         return numbers[left];
    }
}

leetcode运行时间为0ms- 100.00%, 空间为38.6MB - 65.80%

复杂度分析：

时间复杂度：正常情况下二分法的算法复杂度为O(logn), 但是如果这个数组中含有大量重复元素，那么就必须通过right--来缩小范围，这样算法复杂度就降成了O(n)

空间复杂度：需要的空间都是常量级的，所以空间复杂度为O(1)