Lingo简单入门，以及对线性规划做敏感性分析设置

Lingo中用!表示注释，注释结束用;表示，lingo不区分大小写，运行时会自动统一装换成大写

编程步骤：

1.推算出正确的模型

2.确定描述集，定义集合

3.确定变量

4.正确写出每个式子

常用函数（lingo每个函数都必须用@强调）：

!max, min用于用于定义目标函数
@bin(x)表示x为0或1
@gin(x)表示x是整数
@free(x)表示x为任意实数，因为变量默认为非负实数，所以必须用这个函数解除这种限制
@bnd(1, x, u)表示x为[1, u]之间的实数
如表示x在（-5,5)之间的整数，@free(x),@gin(x),@bnd(-5, x, 5)

 编程方法：

1.不使用集合语言--解决小规模问题（笨方法编程）

例如解下面这个线性规划问题

max = 72 * x1 + 64 * x2;
x1 + x2 < 50;
12 * x1 + 8 * x2 < 480;
3 * x1 < 100;
x1, x2 >= 0;

model:
max = 72 * x1 + 64 * x2;
[milk] x1 + x2 < 50;　　　　　　　　!milk是约束条件的别名，方便在结果窗口中查看相关信息;
[time] 12 * x1 + 8 * x2 < 480;　　!time也是别名;
[cpct] 3 * x1 < 100;　　　　　　　　!cpct也是别名;
end

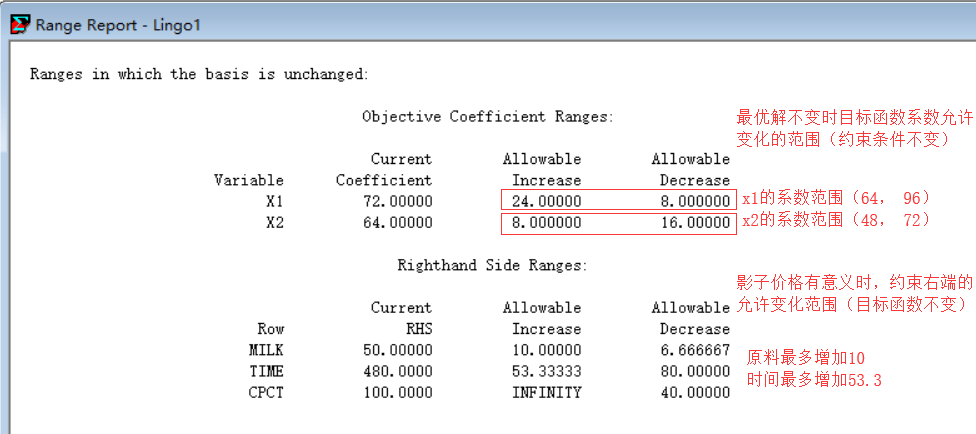
运行结果（会弹出两个窗口,只需关心下面这个窗口，另一个不用管）

2.使用集合语言--解决大规模问题

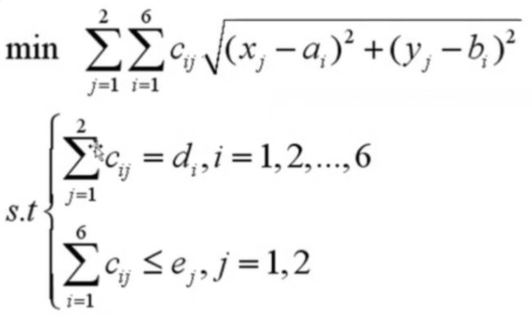
sets: !定义集合;
S/1..6/: a, b, d;    !S集合下标范围是1到6，a b d这三个变量用到了这个集合;
T/1..2/: e, x, y;
U(S, T): c;    !双索引的集合，c用到了这个集合;

endsets    !结束集合的定义;
data:    !定义已知变量,也就是为每个已知变量赋值;

a = 1.25 8.75 0.5 5.75 3 7.25;
b = 1.25 0.75 4.75 5 6.5 7.75;
d = 3 5 4 7 6 11;
x = 5 2;
y = 1 7;
e = 20 20;
enddata    !结束数据的写入;

!目标方程;
min = @sum(T(j):@sum(S(i):c(i, j) * @sqrt((x(j) - a(i))^2 + (y(j) - b(i))^2)));

!约束条件;
@for(S(i):@sum(T(j):c(i, j)) = d(i));    !i属于S集合范围，j属于T集合范围，这个约束条件的意思是在j方向上对Cij求和 == d(i);
@for(T(j):@sum(S(i):c(i, j)) <= e(j));

 教学视屏：https://www.bilibili.com/video/av36145650?from=search&seid=8857491974091223952

(建议1.25倍速）

 对线性规划做敏感性分析设置(这里用第一个题目做样例）

点击lingo -> option -> general solver -> Dura Computations -> Price& ranges -> apply -> save --> ok

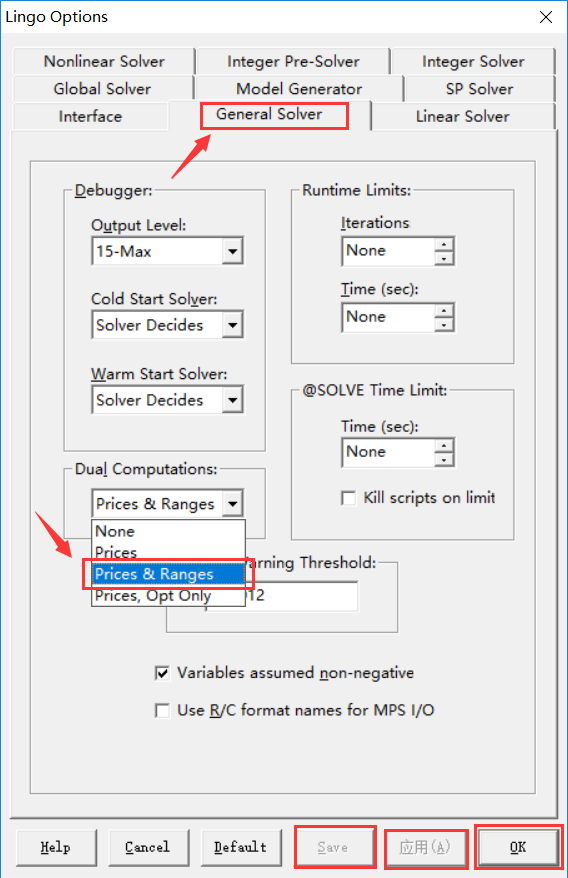
点击lingo -> range