Matlab学习-（1）

1. 认识Matlab

（1）MATLAB是美国MathWorks公司出品的商业数学软件，用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境，主要包括MATLAB和Simulink两大部分。简单来说是数学专用软件，特别适合**处理矩阵**
我大学四年所有的数学计算任务都可以用Matlab完成，可以说这一个软件已经足够你到研究生用了。对很火爆的人工智能也可以用Matlab来建模，已经有相关的资源包，只需要自己搜索就行了。

2. 下载方式

你可以在matlab官网：(https://www.mathworks.com/products/matlab.html)上下载，然后购买正版的。但是正版的很贵，如果不是特别的有钱，最好自己搜索找“免费版”的。我有2016b版的，地址：https://pan.baidu.com/s/1-T1O0Aqal8RjxjzTv_ig3Q，提取码：cb7p。里面有安装教程。
网上的Matlab教程很多，基础语法什么的都是死的，这些东西我没有必要写出来，因为这个就算现在记住了，以后还是会忘。所以我只说最重要的部分，就是教你如何学习。

3. 教程正文

 3.1帮助函数

Matlab中最最重要的东西是函数，这是大学四年写代码后的感觉，有一种说法叫做函数式编程，这个和面向对象有点类似，这两种方法都是可以让代码变得简洁优美，因为我是学数学的，对简单而优美的东西特别喜欢！下面有四种方法来让你知道一个函数怎么用
（1）使用help+函数命令的方式，查看某一函数的介绍。以plot绘图函数为例，在命令行窗口输入help plot，便可得到plot函数的有关介绍。
（2）使用edit+函数命令的方式，查看某一函数的介绍。以plot绘图函数为例，在命令行窗口输入edit plot，同样得到plot函数的有关介绍，只不过这是查看的plot函数的m文件。
（3）使用doc+函数命令的方式，查看某一函数的介绍。以plot绘图函数为例，在命令行窗口输入doc plot，同样得到plot函数的有关介绍，只不过这是通过MATLAB帮助系统（帮助文档）查看的plot函数介绍。
（4）使用lookfor+函数命令的方式，查看某一函数的介绍。以plot绘图函数为例，在命令行窗口输入lookfor plot，此时将出现所有与plot函数有关的M文件，从中找plot，点击查看plot的介绍。
（5）这个是我自己摸索出来的方法，你可以先把某个函数名字先打出来，然后再左键选中这个函数的名字点击右键，有一个查看函数的命令。

3.2 面板的使用

这是我的面板，要注意的东西已经标注了。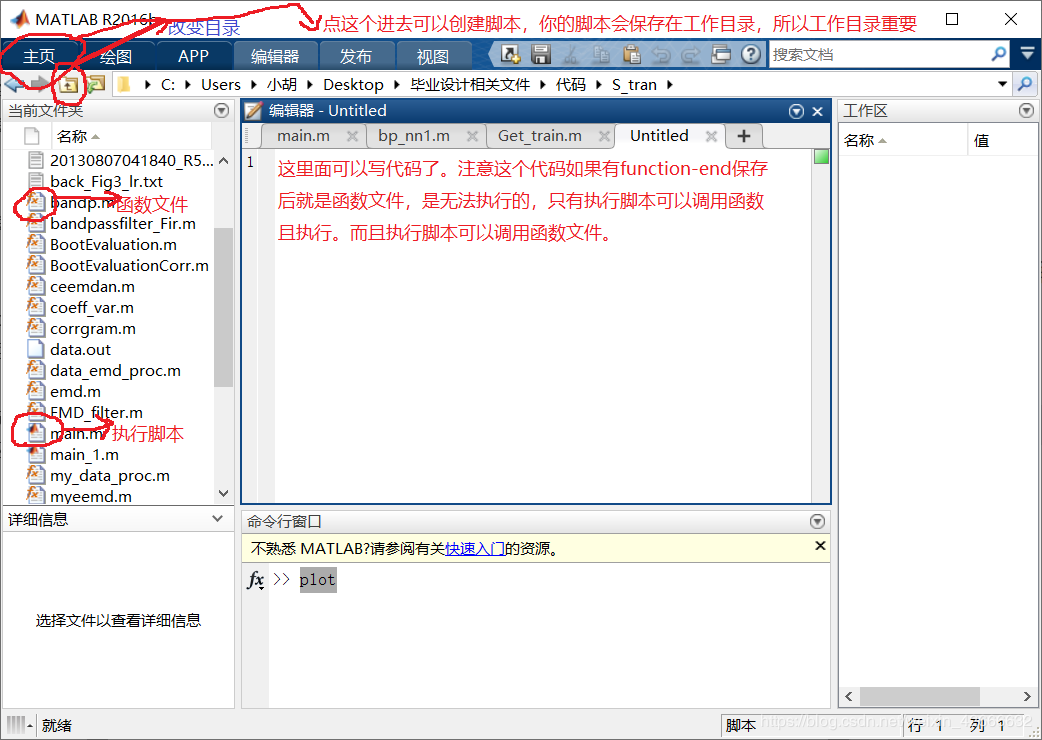

3.3 函数创建

类似C的hello，world！你也可以创建一个函数啦！
点击开始—新建脚本写下面的代码。
然后保存在当前工作目录。

function [a,b]=Hello()
a='Hello,World!';
b='Hello!';
end

保存后在下面的命令行窗口输入：

[a,b]=Hello()

你会得到a和b的值，和这个类似的，你同样可以创建其他的函数，并且调用它了！

3.4 代码调试

 代码调试可可以说是每一个程序员应该掌握的技能。

本文基于MATLAB给出代码调试的方法：

（1）断点法

  细心的人可能发现，当你在调用其他函数的时候，其他函数的变量最后是会被消除的，它们也是局部变量。

 但是假如你有这方面的需求，那么你可以尝试下面几个步骤。

 首先，运行一遍代码，把应该有的变量加载到MATLAB中。

 其次，你得加断点，例如我现在在神经网络函数中加断点：

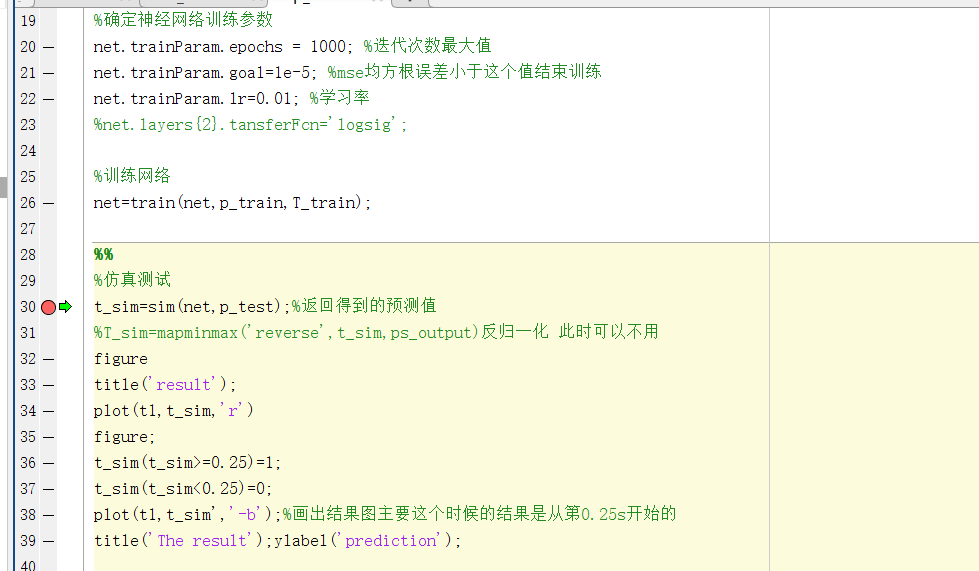
 最后 回到主函数中，右键选中神经网络函数调用的那一部分，点击执行所选代码，就会跳到断点处，然后你就可以看到局部变量了。其他语言也类似。