蒙特卡罗方法 python 实现

蒙特卡罗（Monte Carlo）方法的精髓：用统计结果去计算频率，从而得到真实值的近似值。

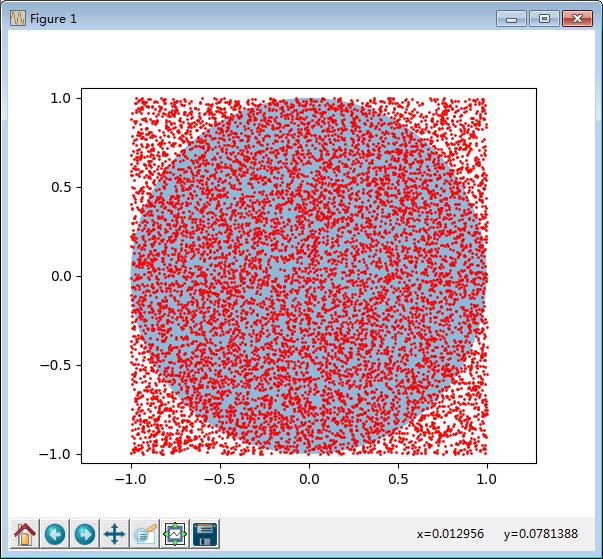
一、求圆周率的近似值，采用 投点法

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Circle

# 投点次数
n = 10000

# 圆的信息
r = 1.0         # 半径
a, b = (0., 0.) # 圆心

# 正方形区域边界
x_min, x_max = a-r, a+r
y_min, y_max = b-r, b+r

# 在正方形区域内随机投点
x = np.random.uniform(x_min, x_max, n) # 均匀分布
y = np.random.uniform(y_min, y_max, n)

# 计算 点到圆心的距离
d = np.sqrt((x-a)**2 + (y-b)**2)

# 统计 落在圆内的点的数目
res = sum(np.where(d < r, 1, 0))

# 计算 pi 的近似值（Monte Carlo方法的精髓：用统计值去近似真实值）
pi = 4 * res / n

print('pi: ', pi)

# 画个图看看
fig = plt.figure() 
axes = fig.add_subplot(111) 
axes.plot(x, y,'ro',markersize = 1)
plt.axis('equal') # 防止图像变形

circle = Circle(xy=(a,b), radius=r, alpha=0.5)
axes.add_patch(circle)

plt.show()

效果图

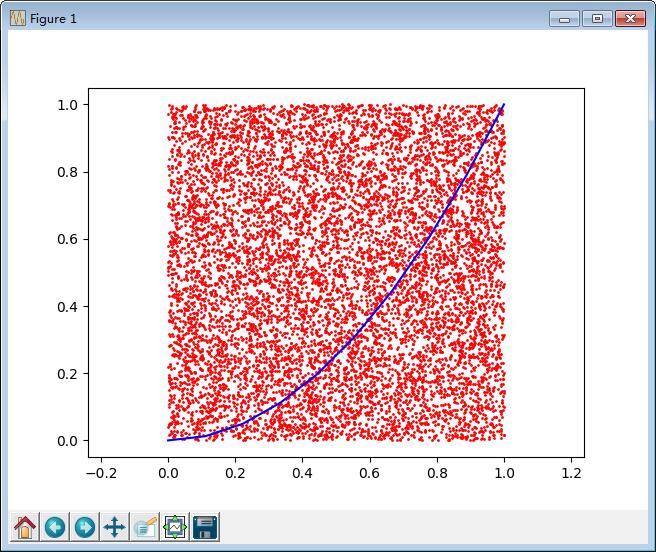
二、求定积分（definite integral）的近似值，采用 投点法

import numpy as np
import matplotlib.pyplot as plt

'''蒙特卡罗方法求函数 y=x^2 在[0,1]内的定积分（值）'''
def f(x):
    return x**2

# 投点次数
n = 10000

# 矩形区域边界
x_min, x_max = 0.0, 1.0
y_min, y_max = 0.0, 1.0     

# 在矩形区域内随机投点
x = np.random.uniform(x_min, x_max, n) # 均匀分布
y = np.random.uniform(y_min, y_max, n)

# 统计 落在函数 y=x^2图像下方的点的数目
res = sum(np.where(y < f(x), 1, 0))

# 计算 定积分的近似值（Monte Carlo方法的精髓：用统计值去近似真实值）
integral = res / n

print('integral: ', integral)

# 画个图看看
fig = plt.figure() 
axes = fig.add_subplot(111) 
axes.plot(x, y,'ro',markersize = 1)
plt.axis('equal') # 防止图像变形

axes.plot(np.linspace(x_min, x_max, 10), f(np.linspace(x_min, x_max, 10)), 'b-') # 函数图像
#plt.xlim(x_min, x_max)

plt.show()

效果图