基于梯度下降的神经网络

一、特点：

0.无监督的神经网络
1.基于梯度下降
2.固定学习速率
3.离线学习（批量学习）
4.隐藏层数目范围：[1, +∞)
4.可以选择激活函数类型
5.numpy的矩阵运算（黑科技）
6.友好的 API （高仿sklearn, 没办法，太好用了 ^_^!!!）
7.测试用到了sklearn库的datasets获取数据，未安装的朋友pip安装即可
8.神经网络学习过程的形象描述：正向传播、反向传播像海浪一样来回冲刷权值W与偏置b
9.用数组的形式实现各层的权值（矩阵）和偏置（向量），其好处是可以用循环来处理各个层。从而可以对隐藏层的数目没有了限制！！附图：


10.忍不住再补充一个想法：上面这个图可以泛化应用到各种循环流水作业的场景

二、效果：
未分类：


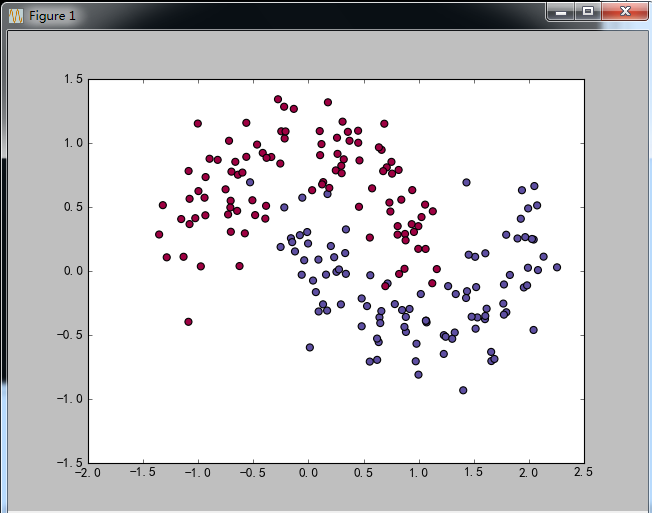
隐藏层：[6,4]效果：

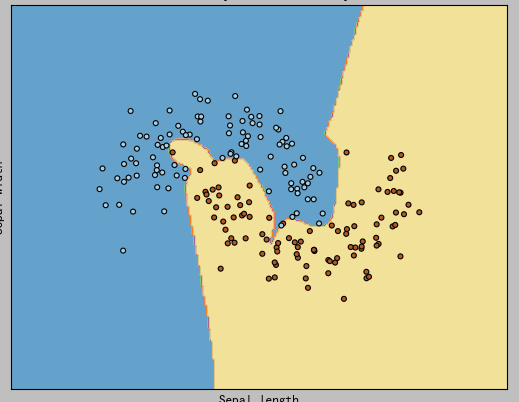
隐藏层：[6,5,3]效果：

隐藏层：[6,8,5]效果：

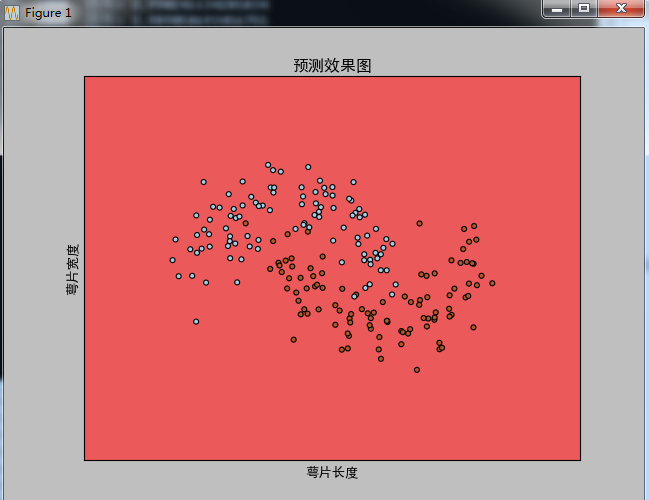
隐藏层：[7,9,12,8,5]效果：（看来不是隐藏层越多，效果越好啊！）

三、代码：

import numpy as np

'''
无监督的神经网络
1.基于梯度下降
2.固定学习速率
3.离线学习（批量学习）
4.可以选择激活函数类型
5.numpy强大的矩阵运算能力
'''

class NeuralNetworks(object):
    '''
    神经网络
        用法：
        >>> X = np.array([[0,0],[0,1],[1,0],[1,1]])
        >>> y = np.array([0,1,2,3])
        
        >>> hiden_layers = [4,6]
        >>> active_type = ['sigmoid', 'sigmoid', 'sigmoid']
        >>> nn = NeuralNetworks(hiden_layers, active_type)
        >>> nn.fit(X, y)
        >>> print(nn.predict(X))
    '''
    def __init__(self, hiden_layers=None, active_type=None, n_iter=10000, epsilon=0.01, lamda=0.01, only_hidens=True):
        '''接收部分参数'''
        self.epsilon = epsilon  # 学习速率
        self.lamda = lamda      # 正则化强度
        self.n_iter = n_iter    # 迭代次数
        if hiden_layers is None:
            hiden_layers = [5] # 默认：隐藏层数目1，节点数目5
        self.hiden_layers = hiden_layers # 各隐藏层节点数 (list)
        self.only_hidens = only_hidens # 接收的是否仅仅是隐藏层，默认True
        
        # 激活函数类型
        self.active_functions = {
            'sigmoid': self._sigmoid,
            'tanh': self._tanh, # 只有这个激活函数才有效果！！
            'radb': self._radb,
            #'line': self._line, #会出错！
        }
        
        # 激活函数的导函数类型
        self.derivative_functions = {
            'sigmoid': self._sigmoid_d,
            'tanh': self._tanh_d,
            'radb': self._radb_d,
            #'line': self._line_d,
        }
        
        if active_type is not None:
            self.active_type = active_type
        else:
            length = len(self.hiden_layers)
            length = length + 1 if self.only_hidens else length - 1
            self.active_type = ['tanh'] * length # 默认激活函数类型
            print(length)
            print(self.active_type)
            
    def _sigmoid(self, z):
        if np.max(z) > 600:
            z[z.argmax()] = 600
        return 1.0 / (1.0 + np.exp(-z))
            
    def _tanh(self, z):
        return (np.exp(z) - np.exp(-z)) / (np.exp(z) + np.exp(-z))
            
    def _radb(self, z):
        return np.exp(-z * z)
            
    def _line(self, z):
        return z
            
    def _sigmoid_d(self, z):
        return z * (1.0 - z)
            
    def _tanh_d(self, z):
        return 1.0 - z * z
            
    def _radb_d(self, z):
        return -2.0 * z * np.exp(-z * z)
            
    def _line_d(self, z):
        return np.ones(z.size) # 全一
        
    def _build(self, X, y):
        '''构建网络'''
        self.X = X
        self.y = y
        
        # 变量
        self.n_examples = y.size            # 样本集数目
        self.n_features = X[0].size         # 样本特征数目
        self.n_classes = np.unique(y).size  # 样本类别数目
        
        all_layers = [] # 各层节点数目（输入、隐藏、输出） 其中隐藏层可多个！！
        if self.only_hidens:
            all_layers.append(self.n_features)
            all_layers.extend(self.hiden_layers)
            all_layers.append(self.n_classes)
        else:
            all_layers.extend(self.hiden_layers)
        
        # 节点数目 (向量)
        self.n = np.array(all_layers) # 如：[3, 4, 2]
        self.size = self.n.size # 层的总数，如上：3
        
        # 层 (向量)
        self.a = np.empty(self.size, dtype=object)
        self.delta_a = np.empty(self.size, dtype=object)
        
        # 偏置 (向量)
        self.b = np.empty(self.size - 1, dtype=object)# 先占位(置空)，dtype=object ！如下皆然
        self.delta_b = np.empty(self.size - 1, dtype=object)

        # 权 (矩阵)
        self.W = np.empty(self.size - 1, dtype=object)
        self.delta_W = np.empty(self.size - 1, dtype=object)

        # 填充
        mu, sigma = 0, 0.1 # 均值、方差
        for i in range(self.size):
            self.a[i] = np.ones(self.n[i])
            self.delta_a[i] = np.zeros(self.n[i])
            if i < self.size - 1:
                self.b[i] = np.ones(self.n[i+1])   # 全一
                self.W[i] = np.random.normal(mu, sigma, (self.n[i], self.n[i+1]))  # # 正态分布随机化
                self.delta_b[i] = np.zeros(self.n[i+1]) 
                self.delta_W[i] = np.zeros((self.n[i], self.n[i+1]))

    def _forward(self, X):
        '''前向传播（批量）'''
        self.a[0] = X # 便于使用循环
        for i in range(self.size - 1):
            nets = np.dot(self.a[i], self.W[i]) + self.b[i]
            #self.a[i+1] = np.tanh(nets)
            self.a[i+1] = self.active_functions[self.active_type[i]](nets) # 加了激活函数
        
        exp_scores = np.exp(nets) # 注意这里还是 nets!!
        probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)
        return probs
        
    def _backward(self, probs):
        '''反向传播（批量）'''
        last = self.size - 1
        
        self.delta_a[last] = probs
        self.delta_a[last][range(self.n_examples), self.y] -= 1
        for i in range(last - 1, -1, -1):
            # 注意：因为是全部样本，所以有些地方要转置，或者前后换位
            self.delta_W[i] = np.dot(self.a[i].T, self.delta_a[i+1])
            self.delta_b[i] = np.sum(self.delta_a[i+1], axis=0)
            #self.delta_a[i] = np.dot(self.delta_a[i+1], self.W[i].T) * (1 - self.a[i]**2)
            self.delta_a[i] = np.dot(self.delta_a[i+1], self.W[i].T) * self.derivative_functions[self.active_type[i]](self.a[i]) # 加了激活函数的导函数
            
            # 正则化
            self.delta_W[i] += self.lamda * self.W[i]
            #self.delta_b[i] += 0.0
            
            # 梯度下降
            self.W[i] += -self.epsilon * self.delta_W[i]
            self.b[i] += -self.epsilon * self.delta_b[i]

    def _calculate_loss(self):
        '''损失函数（批量）'''
        probs = self._forward(self.X) # 批量: self.X
        
        # 计算损失
        corect_logprobs = -np.log(probs[range(self.n_examples), self.y])
        data_loss = np.sum(corect_logprobs)
        
        # 添加正则项损失(可选)
        data_loss += self.lamda/2 * (sum([np.sum(np.square(w)) for w in self.W]))
        return 1./self.n_examples * data_loss
        
    def fit(self, X, y):
        '''拟合'''
        # 将神经网络搭建完整
        self._build(X, y)
        
        # 按迭代次数，依次：
        for i in range(self.n_iter):
            # 前向传播
            probs = self._forward(self.X)
            # 反向传播
            self._backward(probs)
            # 计算损失
            if i % 1000 == 0:
                loss = self._calculate_loss()
                print("迭代次数：{}	损失: {}".format(i, loss))

    def predict(self, x):
        '''预测（批量）'''
        probs = self._forward(x)
        return np.argmax(probs, axis=1)
        
        
# 以下皆为测试
#>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
def plot_decision_boundary(plt, xx, yy, Z, X, y, title):
    '''作图函数'''
    # 等高线图
    plt.contourf(xx, yy, Z, cmap=plt.cm.Paired, alpha=0.8)
    # 散点图
    plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired)
    
    plt.xlabel('萼片长度')
    plt.ylabel('萼片宽度')
    plt.xlim(xx.min(), xx.max())
    plt.ylim(yy.min(), yy.max())
    plt.xticks(())
    plt.yticks(())
    plt.title(title)
    plt.show()
    
def test2():
    '''第二个测试函数'''
    import matplotlib.pyplot as plt
    from sklearn import datasets
    # --------------------------------------------
    # 解决matplotlib中文乱码
    plt.rcParams['font.sans-serif'] = ['SimHei']
    plt.rcParams['axes.unicode_minus'] = False
    # --------------------------------------------
    
    # ======================================================
    # 生成数据
    np.random.seed(0)
    X, y = datasets.make_moons(200, noise=0.20)

    h = .02
    x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                         np.arange(y_min, y_max, h))
    # ======================================================
    
    # 先作散点图，看看数据特点
    plt.scatter(X[:,0], X[:,1], s=40, c=y, cmap=plt.cm.Spectral)
    plt.show()

    # 定义神经网络
    nn = NeuralNetworks([6,5,3])
    # 拟合
    nn.fit(X, y)
    # 预测
    Z = nn.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    # 作图
    plot_decision_boundary(plt, xx, yy, Z, X, y, "预测效果图")

def test1():
    '''第一个测试函数'''
    # 第一步：准备数据
    # 说明：逻辑异或（XOR）
    X = np.array([[-1,-1],[-1,1],[1,-1],[1,1]])
    y = np.array([0,1,2,3])
    
    # 第二步：创建神经网络
    # 说明：1.两个隐藏层，节点数目分别为4、6有两个节点
    #       2.输入层和输出层节点数目自动识别，默认不输入
    #       3.若包含输入层与输出层，可以设置参数 only_hidens=True
    #         如：nn = NeuralNetworks([2, 4, 6, 4], only_hidens=True)
    #
    #       4.完整例子：nn = NeuralNetworks(hiden_layers=[4, 6],
    #                                       active_type = ['tanh', 'tanh', 'tanh'], 
    #                                       n_iter=10000, 
    #                                       epsilon=0.01, 
    #                                       lamda=0.01, 
    #                                       only_hidens=True)
    nn = NeuralNetworks([2, 4, 6, 4], active_type = ['tanh', 'tanh', 'sigmoid'], only_hidens=False)
    
    # 第三步：拟合
    nn.fit(X, y)
    
    # 第四步：预测
    print(nn.predict(X))
    
    
if __name__ == '__main__':
    test1()
    test2()