本文是学习数据结构的笔记。
【效果图】
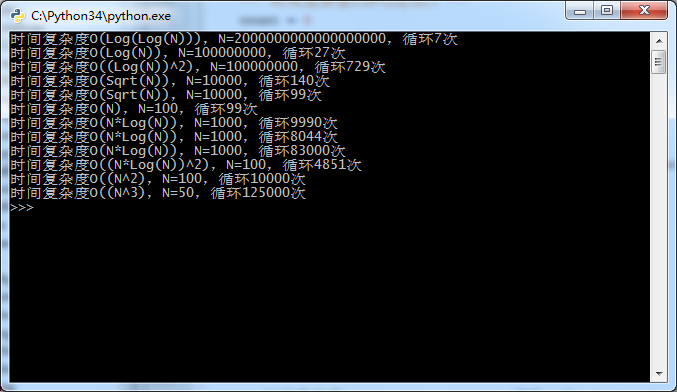
【代码】
# example.py # 算法时间复杂度示例 def func_01(n): ''' 时间复杂度O(Log(Log(N))) ''' import math i = n count = 0 while i > 1: i = round(math.sqrt(i)) # 注意:sqrt(i)! count += 1 return count print('时间复杂度O(Log(Log(N))),N=2000000000000000000,循环{}次'.format(func_01(2000000000000000000))) def func_02(n): ''' 时间复杂度O(Log(N)) ''' i = n count = 0 while i >= 1: i = i // 2 # 注意:// 2! count += 1 return count print('时间复杂度O(Log(N)),N=100000000,循环{}次'.format(func_02(100000000))) def func_03(n): ''' 时间复杂度O((Log(N))^2) ''' i = 1 count = 0 while i <= n: j = n while j > 0: j = j // 2 # 注意:// 2! count += 1 i = i * 2 # 注意:* 2! return count print('时间复杂度O((Log(N))^2),N=100000000,循环{}次'.format(func_03(100000000))) def func_04_01(n): ''' 时间复杂度O(Sqrt(N)) ''' i = s = 1 count = 0 while s < n: i = i + 1 s = s + i count += 1 return count print('时间复杂度O(Sqrt(N)),N=10000,循环{}次'.format(func_04_01(10000))) def func_04_02(n): ''' 时间复杂度O(Sqrt(N)) ''' i = 1 count = 0 while i * i < n: count = count + 1 i = i + 1 return count print('时间复杂度O(Sqrt(N)),N=10000,循环{}次'.format(func_04_02(10000))) def func_05(n): ''' 时间复杂度O(N) ''' count = 0 for i in range(1, n): count += 1 return count print('时间复杂度O(N),N=100,循环{}次'.format(func_05(100))) def func_06_01(n): ''' 时间复杂度O(N*Log(N)) ''' count = 0 for i in range(1, n): j = 1 while j <= n: j = j * 2 # 注意:* 2! count += 1 return count print('时间复杂度O(N*Log(N)),N=1000,循环{}次'.format(func_06_01(1000))) def func_06_02(n): ''' 时间复杂度O(N*Log(N)) ''' count = 0 for i in range(1, n): j = 1 while j < n: j = j + i # 注意: + i! count = count + 1 return count print('时间复杂度O(N*Log(N)),N=1000,循环{}次'.format(func_06_02(1000))) def func_06_03(n): ''' 时间复杂度O(N*Log(N)) ''' count = 0 for i in range(1, n // 3): # 注意:// 3! j = 1 while j <= n: j = j + 4 # 注意:+ 4! count = count + 1 return count print('时间复杂度O(N*Log(N)),N=1000,循环{}次'.format(func_06_03(1000))) def func_07(n): ''' 时间复杂度O(N*(Log(N))^2) ''' count = 0 for i in range(1, n): j = 1 while j <= n: k = 1 while k <= n: count += 1 k = k * 2 # 注意:* 2! j = j * 2 # 注意:* 2! return count print('时间复杂度O((N*Log(N))^2),N=100,循环{}次'.format(func_07(100))) def func_08(n): ''' 时间复杂度O(N^2) ''' count = 0 for i in range(n): for j in range(n): count += 1 return count print('时间复杂度O((N^2),N=100,循环{}次'.format(func_08(100))) def func_09(n): ''' 时间复杂度O(N^3) ''' count = 0 for i in range(n): for j in range(n): for k in range(n): count += 1 return count print('时间复杂度O((N^3),N=50,循环{}次'.format(func_09(50)))