P1345 [USACO5.4]奶牛的电信Telecowmunication
题目描述
农夫约翰的奶牛们喜欢通过电邮保持联系,于是她们建立了一个奶牛电脑网络,以便互相交流。这些机器用如下的方式发送电邮:如果存在一个由c台电脑组成的序列a1,a2,...,a(c),且a1与a2相连,a2与a3相连,等等,那么电脑a1和a(c)就可以互发电邮。
很不幸,有时候奶牛会不小心踩到电脑上,农夫约翰的车也可能碾过电脑,这台倒霉的电脑就会坏掉。这意味着这台电脑不能再发送电邮了,于是与这台电脑相关的连接也就不可用了。
有两头奶牛就想:如果我们两个不能互发电邮,至少需要坏掉多少台电脑呢?请编写一个程序为她们计算这个最小值。
以如下网络为例:
1* / 3 - 2*
这张图画的是有2条连接的3台电脑。我们想要在电脑1和2之间传送信息。电脑1与3、2与3直接连通。如果电脑3坏了,电脑1与2便不能互发信息了。
输入输出格式
输入格式:
第一行 四个由空格分隔的整数:N,M,c1,c2.N是电脑总数(1<=N<=100),电脑由1到N编号。M是电脑之间连接的总数(1<=M<=600)。最后的两个整数c1和c2是上述两头奶牛使用的电脑编号。连接没有重复且均为双向的(即如果c1与c2相连,那么c2与c1也相连)。两台电脑之间至多有一条连接。电脑c1和c2不会直接相连。
第2到M+1行 接下来的M行中,每行包含两台直接相连的电脑的编号。
输出格式:
一个整数表示使电脑c1和c2不能互相通信需要坏掉的电脑数目的最小值。
输入输出样例
输入样例#1: 复制
3 2 1 2
1 3
2 3
输出样例#1: 复制
1
题解
今天正好讲网络流。
(北大学长鬼畜地题目让我发现自己基本都不会做)
那就打打板子题吧。
这道题是最小割点模板。
每个点很显然会影响到与它相连的边啊。
那么要怎么处理呢?
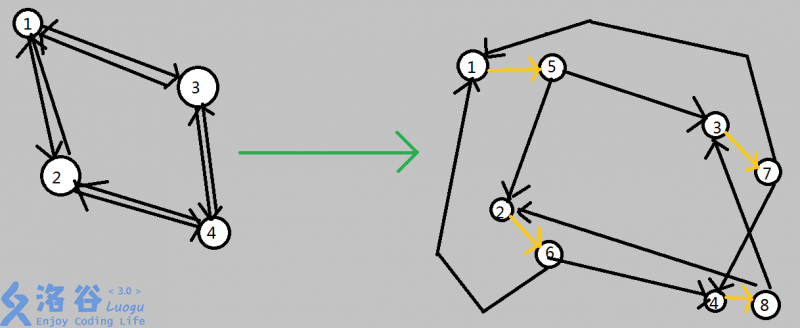
如图,我只需要新加一条 (i) 到 (i+n) 的边就可以了。
流入(i),流入为(i+n).
断开这条边时就留不通了,同等于断点。
代码
#include<cstdio>
#include<cstring>
#include<cmath>
#include<queue>
#include<algorithm>
#include<iostream>
using namespace std;
const int N=100001;
struct node{
int next,c,to;
}e[N<<1];
int num=1,head[N],dep[N];
int n,m,s,t;
int read()
{
int x=0,w=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return x*w;
}
void add(int from,int to,int c){
num++;
e[num].to=to;
e[num].c=c;
e[num].next=head[from];
head[from]=num;
}
bool bfs(){
memset(dep,0,sizeof(dep));
queue<int>q;q.push(s);dep[s]=1;
while(!q.empty()){
int u=q.front();q.pop();
for(int i=head[u];i;i=e[i].next){
int v=e[i].to;
if(!dep[v]&&e[i].c)dep[v]=dep[u]+1,q.push(v);
}
}
return dep[t];
}
int dfs(int x,int cap){
if(x==t)return cap;
int addx=0;
for(int i=head[x];i;i=e[i].next){
int v=e[i].to;
if(dep[v]==dep[x]+1&&e[i].c){
int tmp=dfs(v,min(cap-addx,e[i].c));
e[i].c-=tmp;e[i^1].c+=tmp;addx+=tmp;
}
}
return addx;
}
int dinic(){
int ans=0;
while(bfs())ans+=dfs(s,10000000);
return ans;
}
int main()
{
n=read();m=read();s=read();t=read();
for(int i=1;i<=n;i++)add(i,i+n,1),add(i+n,i,0);
for(int i=1;i<=m;i++){
int x=read(),y=read();
add(y+n,x,999999);add(x,y+n,0);
add(x+n,y,999999);add(y,x+n,0);
}
s+=n;
printf("%d",dinic());
return 0;
}