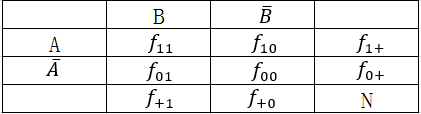关联分析方法具有产生大量模式的潜在能力,在真正的商业数据上,数据量与数据维数都非常大,很容易产生数以千计、万计甚至百万计的模式,而其中很大一部分可能并不让人感兴趣,筛选这些模式,以识别最有趣的模式并非一项平凡的任务,因为“一个人的垃圾在另一个人那里可能就是财富”,因此建立一组广泛接受的评价关联模式质量的标准是非常重要的。评价标准可以通过客观统计论据建立,例如上一篇提到过得支持度与置信度等,也可以通过主观论据建立,例如一些专家经验知识等。
1.客观统计论据
利用客观统计论据评价模式时,一般通过计算模式的客观兴趣度来度量,而这样的度量一般是基于相依表(contingency table)得到,下表是一对二元变量、
的相依表,用
表示
不出现在事务记录中
表示
和
均出现在事务记录中的次数,
表示
出现、
未出现在事务记录中的次数,
表示
出现、
未出现在事务记录中的次数,
表示
和
均未出现在事务记录中的次数,
表示
出现在事务记录中的次数,
表示
未出现在事务记录中的次数,
表示
出现在事务记录中的次数,
表示
未出现在事务记录中的次数,
表示事务记录的总数。
1.1 支持度
支持度用于筛选出频繁项集,但是该度量有一个缺点,一些支持度较低、但让人感兴趣的模式会被忽略掉,模式毕竟是只出现在部分数据中的,因此使用支持度度量可能会出现这种情况。
1.2 置信度
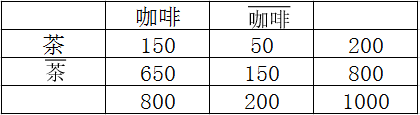
置信度用于评估规则的可信程度,但是该度量有一个缺点,没有考虑规则后件的支持度问题,例如在下面的相依表中
规则{茶}{咖啡}的支持度为15%,置信度为75%,先不考虑支持度,只看置信度会觉得比较高,因为可能会认为爱喝茶的人一般也爱喝咖啡。我们再来看一下喝咖啡的人的支持度,达到80%,规则{茶}
{咖啡}的置信度75%高,这说明什么问题?并不是爱喝茶的人一般爱喝咖啡,从而使得规则置信度高,而是爱喝咖啡的人本身就很多,所以这条规则是一个误导。
1.3 提升度与兴趣因子
由于置信度存在的缺陷,人们又提出了称作提升度的度量:
提升度定义为规则置信度与规则后件支持度的比率。对于二元变量,提升度等价于兴趣因子
兴趣因子比较的是模式的频率与统计独立假设下计算的基线频率,对于相互独立的两个变量,其基线频率定义为:
从这个角度,可以将兴趣因子解释如下:
在1.2节的例子中,规则{茶}{咖啡}的兴趣因子为
,这表明喝茶的人数与喝咖啡的人数之间呈负相关,因此这条规则是不合理的。
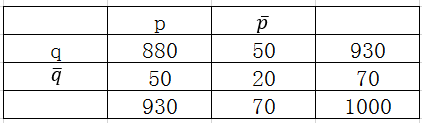
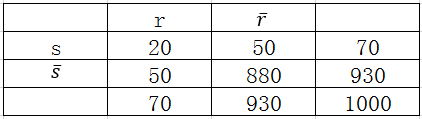
使用提升度与兴趣因子来评判规则有一个问题,我们以提升度为例来说明,当规则置信度与规则后件支持度数值大小相近时,提升度就不足以说明问题,比率的形式掩盖了分子、分母本身的数值大小。例如下面这个例子,有两个相依表与
如下
如果仅仅用提升度来评判规则,那么显而易见的是规则优于
,但是我们评判规则优劣时还应该具体到任务场景中,例如在文本挖掘中,经常用一对词语同时出现在文档中的频数来分析这对词语的关联程度,在这种情况下,提升度就不是一个最佳度量。
1.4 相关分析
相关分析是一种基于统计学的技术,在之前《数据测量与相似性分析》的博文中曾经说明过,对于连续型变量,相关度用皮尔森相关系数表示(https://blog.csdn.net/huguozhiengr/article/details/83033465),对于二元变量,相关度可以用系数度量
相关度的值从-1(完全负相关)到+1(完全正相关),如果变量是相互独立的,那么相关度为0。如果变量是正相关,那么应该大于
、
应该大于
,因此相关度大于0,同理,如果变量负相关,相关度应该小于0。
使用相关分析评判规则时,存在一定局限性,相关分析中把事务记录中项的出现于不出现视为同等重要,例如在1.3节的例子中,,
,二者相同,因此相关分析更适合于分析对称的二元变量。
1.5 IS度量
度量用于处理非对称二元变量,其定义如下:
从该定义式中可以看出,当规则的兴趣因子与支持度都很大时,度量值就很大。在1.3节的例子中,
,
,可以看到在此情况下
度量给出的结果与兴趣因子与
系数相反。在分析兴趣因子时,我们提到比率的形式掩盖了分子、分母本身数值的大小,而在
度量中则考虑到了规则的支持度,这在一定程度上弥补了兴趣因子的不足之处。
度量也存在与置信度类似的局限性——即使是不相关或者负相关的模式,也能得到较大的
度量,当两个变量独立时
由于和
均小于1,因此得到
度量小于各自的支持度。关于这个局限性也可以这样理解,
度量的定义式变换如下
可以看到度量表示成了规则
与
的几何均值。
1.6 其它客观兴趣度度量
2.客观兴趣度度量的性质
从第1节中举的几个简单例子中就可以看出,在一种情况下不同度量给出的结果可能会相差很大,甚至是矛盾的,而在更复杂的实际情况中,这种情况更是常见,因此有必要研究一下客观兴趣度度量的性质。
2.1 反演性
事务记录A、B、C、D分别如下,1表示某一项存在,0表示不存在
| A | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| B | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| C | 0 | 1 | 1 | 1 | 1 | 1 | 0 |
| D | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
查看该事务记录表发现,记录C与记录A的购买内容刚好相反,记录D与记录B的购买内容刚好相反, 在事务记录表中这种操作称为反演。在两个事务记录呈反演的数据集中,相依表中的、
、
、
数值刚好相反,若此时客观度量在这两个数据集中结果不变,则称该度量满足反演性,满足反演性的度量有
系数、几率、集体强度,而前面介绍的兴趣因子和
等度量则不满足反演性。
在二元变量中,反演性讨论的是变量对称性问题下的度量问题,显然,满足反演性的度量更适合于对称的二元变量数据事务集中,在非对称的二元变量数据集中,不满足反演性的度量则更适合。
2.2 零加性
在事务记录中,有一些既没有出现规则中的前件,也没有出现后件,这样的记录是与规则无关的,被统计在相依表的项中。在数据记录集中添加一些与规则无关的记录,称为零加操作。如果在零加操作下(即增加
的值,而其它项频数保持不变),客观度量仍然保持不变,则称该客观度量满足零加性。
我们搜集到的数据集中不可避免的会包含一些多余的数据(当然,数据的多余是相对于规则而言的),如果这些多余的数据影响到了规则的挖掘与评定,如果我们就要考量一下选用的挖掘方法与客观度量是否合适。满足零加性的度量有余弦度量()、Jaccard度量。
2.3 缩放性
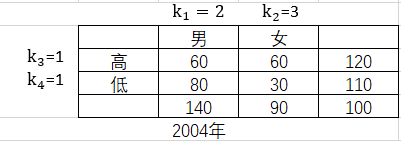
下表是1993年与2004年注册某课程的学生的性别与成绩的相依表,表中的数据表明,自1993年来男生的数量翻了一番,而女生的数量则是以前的3倍,然后2004年的男生、女生的表现并不比1993年的表现得更好,因为高分与低分的男同学比例保持不变,女同学也是这样。
、
、
、
表示对相依表中的行和列的缩放倍数。若对相依表中
、
、
、
进行缩放之后,客观度量保持不变,则称该度量具有缩放不变性,在以上介绍的度量中(包括图片中的客观度量),只有几率(
)满足缩放不变性。
3.主观论据
在评估关联模式时引入主观信息是一件比较困难的事情,这需要来自领域专家的大量先验信息,常见的一些将主观信息加入到模式发现任务中的方位有以下几种:
- 可视化方法:通过数据可视化方法呈现出数据中蕴含的信息,领域专家由此解释和检验发现的模式,只有符合观察到的信息的模式才被认为是有趣的。
- 基于模板的方法:这种方法可以限制发现的模式类型,只有满足指定模板的模式才被认为是有趣的。
- 主观兴趣度量:基于领域信息定义一些主观度量来过滤显而易见和没有实际价值的模式。
4.辛普森悖论
在介绍 分类:贝叶斯分类方法 中就提到过,我们在分析中可能会忽略掉一些隐藏变量,而这些变量对分析结果影响较大,在关联模式挖掘中,这就可能导致观察到的一对变量间的联系消失或者逆转,这种现象就是所谓的辛普森悖论。下面通过一个例子说明这种现象。
考虑高清电视(HDTV)销售与健身器材销售之间的联系。在下列相依表中,规则 {买HDTV=是}{买健身器材=是}的置信度为99/180=55%,而规则{买HDTV=否}
{买健身器材=是}的置信度为54/120=45%,该规则暗示买HDTV的人更可能买健身器材(这里举置信度的例子只是为了说明辛普森悖论现象,很明显以上两个规则的置信度均不高,不足以成为规则)。
| 买HDTV | 买健身器材 | ||
| 是 | 否 | ||
| 是 | 99 | 81 | 180 |
| 否 | 54 | 66 | 120 |
| 153 | 147 | 300 | |
如果将购买这两种物品的人群 大学生、在职人员,那么会得到下列相依表
| 顾客组 | 买HDTV | 买健身器材 | 总数 | |
| 是 | 否 | |||
| 大学生 | 是 | 1 | 9 | 10 |
| 否 | 4 | 30 | 34 | |
| 在职人员 | 是 | 98 | 72 | 170 |
| 否 | 50 | 36 | 86 | |
可以看到,对于大学生:
c({买HDTV=是}{买健身器材=是})=1/10=10%
c({买HDTV=否}{买健身器材=是})=4/34=11.8%
对于在职人员:
c({买HDTV=是}{买健身器材=是})=98/170=57.7%
c({买HDTV=否}{买健身器材=是})=50/86=58.1%
可以看到,在两组人群中,依据规则置信度得到的结论刚好与之前相反,这就是辛普森悖论现象,当然,可能是由于选择的客观度量的原因,所以才会出现这种现象,那么我们用兴趣因子来重新计算一下。
不考虑人群因素影响是,
({买HDTV=是}
{买健身器材=是})= 300*99/(180*153)=1.078
({买HDTV=否}
{买健身器材=是})= 300*54/(120*153)=0.882
依此得到的结论是:买HDTV的人更可能买健身器材
现在考虑人群因素的影响,对于大学生:
({买HDTV=是}
{买健身器材=是})= 44*1/(5*10)=0.88
({买HDTV=否}
{买健身器材=是})= 44*4/(34*5)=1.035
对于在职人员:
({买HDTV=是}
{买健身器材=是})= 256*98/(170*148)=0.997
({买HDTV=否}
{买健身器材=是})= 256*50/(86*148)=1.006
可以看到,得到的结论刚好与之前相反,使用兴趣因子做度量时同样出现了辛普森悖论。(当然,还可以继续使用其它度量算一下,我就不算了,这里只是为了说明问题)
辛普森现象的存在警示我们,在解释变量之间的关联要特别小心,因为一些可能存在、没有考虑的因素可能会影响模式。要做到模式的解释,就需要我们拥有一定的背景知识,拿上面的例子说明,HDTV与健身器材并不是普通物品(这很重要,就像收入低的人群去吃豪华大餐一样,这不是一件很常见的事情),它的购买群体是值得考虑的,最起码得知道是水购买了这些物品。
5.小结
文中介绍规则评估方面的内容,主要是客观度量的介绍,可以看到对于同一个规则,采用不同度量可能会得到相反的结论,这是由于度量的定义导致,没有一个客观度量能适用于所有模式挖掘任务中,因为每种度量总会有一些未考虑的方面,因此在我们的工作中,充分了解、理解数据,运用背景知识显得很重要,有时也可以考虑多种度量结合的方式来帮助我们发现有趣的模式。