K最邻近分类

      最邻近分类是分类方法中比较简单的一种，下面对其进行介绍

1.模型结构说明

       最邻近分类模型属于“基于记忆”的非参数局部模型，这种模型并不是立即利用训练数据建立模型，数据也不再被函数和参数所替代。在对测试样例进行类别预测的时候，找出和其距离最接近的个样例，以其中数量最多的类别作为该样例的类预测结果。

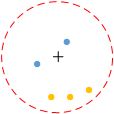
       最邻近分类模型的结构可以用下图来说明，图中叉号表示输入的待分类样例，对其分类时选定一个距离范围（虚线圆圈表示的范围），在该范围内包含有个样例（除去待分类样例外，这里=5），这里所说的距离并不专指距离度量（如曼哈顿距离、欧氏距离等），它可以是任意一种邻近度度量（在我的博文《数据测量与相似性分析》中有介绍），此时最邻近的5个样例中，有3个“+”例，2个“-”例，故待分类样例的类别定位“+”。为了便于确定类别，一般取奇数。

                                                                  ​

        

2.模型构建

     2.1 K值选取

       从最邻近分类方法的分类过程可知，值对模型的误分类率影响较大。较小时，相当于用较小邻域中的样例进行预测，“学习”的近似误差会减小，但是“学习“的估计误差会增大，且对邻域内的样例非常敏感，若邻近的样例中包含部分噪声，预测结果就会出错，较大时的情况则相反。

        总的来说，值减小意味着整体模型变复杂，容易发生过拟合，值增大意味着模型变简单，导致忽略“训练”样例中一些有用信息，预测误分类率会增高。在应用中，一般取较小的值（例如sklearn库中最邻近分类器KNeighborsClassifier中默认为5），可以通过交叉验证法选择一个合适的值

     2.2 最邻近样例搜索

       由于最邻近分类器不需要利用样例进行训练，因此关键点就集中在如何快速进行邻近样例搜索，这在特征空间维数大和样例数据量大时非常重要。一种容易想到的方法是对所有样例进行线性搜索，但显然这在特征空间高维数、样例量大时不可取。有很多方法可以提高搜索效率，这里介绍其中的一种——树(kd tree)方法。

        树（也是一种二叉树）是一种对  维空间中的样例进行存储以便对其进行快速检索的树形结构，在特征空间为一维时，平衡二叉树是一个不错的选择，但是当特征空间为多维时，平衡二叉树就无能为力了，此时  树就派上用场了。

       2.2.1 树构造过程       

       树的构造过程大致为：首先构造一个根节点，选择  维特征空间中的一个变量，依据在变量上的取值的中位数划分样例集（大于或等于中位值、小于中位值），形成左子树和右子树，这个根节点就类似于一个矩形超平面，将样例集划分到平面左右两侧。接着再选择一个变量，按照样例在变量上取值的中位值分别对左子树、右子树中的样例进行划分，这个过程相当于在之前被根节点一分为二的左、右超平面内，分别用基于各自空间内上中位数的矩形超平面再次将子空间进行划分，重复这个过程，直到树的每个结点上只包含一个样例为止（即叶子结点，从几何空间上看，即划分后两个子区域内没有实例存在）。这个过程中有几点需要单独强调：

      (1) 在这个过程中，划分空间时变量优先选择策略可以为：依据子空间内（根节点时为整个样例空间）样例在该变量上取值波动程度（即方差），波动大的优先选择。当然，也可以是随机选择。

      (2) 当所有变量都已被用来划分样例、划分仍未结束时，需要接着用所有变量再进行一次划分，不断重复该过程，直到划分停止。

      (3) 假设当前选择用变量进行划分，那么本次划分是在各子空间单独进行的，即各子空间内本次划分时，在变量上选值是依据该子空间内样例的中位值。

      (4) 树上对同一层深度的样例划分时，必须使用同一变量，也即是说在一次划分中，各子空间必须使用同一变量。

      (5) 划分值（矩形超平面位置）选择的是各子空间内样例在变量上取值的中位数，这种划分策略保证生成的树是平衡的。

      (6) 若训练集中存在标称型属性，使用K最邻近分类器则不太合适，因为标称型属性无法参与到距离度量的计算中。

       2.2.2 树的构造算法

      输入：维空间数据集，其中 

      输出：树

• 开始：构造根节点，根节点对应于包含的  维空间的超矩形区域。选择为坐标轴，以中所有实例的坐标的中位数为切分点，将根节点对应的超矩形区域切分为两个子区域。切分由通过切分点并与坐标轴垂直的超平面实现。对由根结点生成深度为1的左、右子结点，左子结点对应坐标小于切分点的子区域，右子结点对应于坐标大于切分点的子区域。将落在切分超平面上的实例点保存为根节点。
• 重复：对深度为的结点，选择为切分的坐标轴，，以该结点的区域中所有实例的坐标的中位数为切分点，将该结点对应的超矩形区域分为两个子区域。切分由通过切分点并与坐标轴垂直的超平面实现。由该结点生成深度为+1的左、右子结点：左子结点对应坐标小于切分点的区域，右子结点对应坐标大于切分点的区域。将落在切分超平面上的实例点保存在该结点。
• 结束：直到两个区域没有实例存在时停止。

      举一个树构造的例子，给定一个二维空间数据集

                                                

       树的构造过程为：选择轴，6个数据点坐标的中位数为7（5也可以），以平面=7将空间划分为左、右两个子矩形（子结点），左子矩形以=4平面一分为二，右子矩形以=6一分为二，如此递归，得到下图(左)所示的特征空间划分，下图(右)所示的树。

  ​​

      2.2.3 搜索树 

       从树的构造过程来看，可以省去对大部分数据点的搜索，从而减少搜索的时间。给定一个目标点（即待分类样例），先找到包含该目标点的叶子结点，然后依次回退到父结点，在这个过程中不断查找与目标点最邻近的样例，当确定不可能存在更近的结点时，结束搜索过程，这个过程可以用下图来说明（此次搜索过程不涉及图中左下子区域中的点，因此未画出）

                                          ​
       图中共有A、B、C、D、E、F 5个样例点，其中点F(绿色)输入的待分类样例点，点A(根节点，红色，椭圆)在变量的矩形超平面上，点B(红色，圆形)在变量的矩形超平面下方，点C、D、E、F 均在变量的矩形超平面上方。点C(蓝色，椭圆)在变量的矩形超平面上，点D(蓝色，圆形)在变量的矩形超平面左边，点E、F在变量的矩形超平面右边。

      首先找到点F所在的叶子结点，即点E（点F与点E在同一区域内），此时点E为最邻近点，计算点F与点E间的距离，得到(蓝色虚线)。接着回到父结点C上，计算父结点C与点F间的距离，发现该距离大于，故最邻近点仍然为点E，然后以点F为圆心，为半径作圆（蓝色线条的圆），若该圆与变量上的矩形超平面相交，则需要对父结点C的另一个子区域（左子树）内的点进行搜索，因为这表明其中可能存在更邻近点；若圆（蓝色线条的圆）与变量上的矩形超平面不相交，则不必在父结点的另一个子空间内搜索。由于此时圆（蓝色线条的圆）与变量上的矩形超平面相交，因此需要计算点D与点F间的距离(红色虚线)，结果发现，故此时点D是最邻近点。

      接着再回到结点C的父结点A上，计算点A与点F间的距离并与比较，发现该距离大于，故点D仍然为最邻近点，然后以点F为圆心，为半径作圆，该圆与变量的矩形超平面不相交，故不需要再对结点A的左子树（变量的矩形超平面下半区域）内的点进行搜索，即点B不可能是最邻近点。

       至此为止，在本例中搜索过程结束，需要说明的是，本例中的圆在实际多维特征空间中为超球体，判断超球体与分类矩形超平面是否相交的方法为：待分类点（目标点）与分类超矩形平面的距离（即在当前分类变量上，待分类点与父结点在上取值的差值的绝对值）是否大于超球体半径。在实际中也只需要依照该过程不断重复，直至搜索到根节点。

       树上最邻近点的搜索算法为：

• 在 树上找出包含目标点  的叶子结点：从根节点出发，递归的向下访问 树，若目标点  当前维的坐标小于切分点的坐标，则移动到左子树点，否则移动到右子树点，直至子结点为叶子结点为止。
• 以此叶子结点为最邻近点
• 递归的向上回退，在每个结点进行一下操作：
  • 如果该结点保存的实例点比当前最近点距离目标点更近，则以该实例点为“当前最近点”
  • 当前最近点一定存在于该结点的一个子结点对应的区域。检查该子结点父结点的另一子结点对应的区域是否有更近点。具体的，检查另一子结点对应的区域是否与以目标点为球心、以目标点与“当前最近点”间距离为半径的超球体相交。如果相交，可能在另一子结点对应的区域内存在距离目标点更近的点，移动到另一子结点。接着递归的进行最邻近搜索。如果不想交，则向上回退。
• 当退回到根结点时，结束搜索，最后的“当前最近点”即为  的最邻近点。

    

       以上的过程是的情况，对于的情况，搜索的方式和时一样，但在找最近的个点时，首先要保证找到数量足够的点，在前次搜索时不必考虑距离问题，直接将这个点当做“当前最近个点”，接下来的搜索就要考虑距离问题了，以这个点中最远距离作为“当前最近距离”，当找到更近的点时，对“当前最近距离”进行更新。

3.对距离进行加权处理

        当数据中类分布不平衡时，会出现以下这种情况，假设

                                                                                  ​

       蓝色的点表示类1，橙色的点表示类2，依据KNN算法中对类别的判定规则，此时样本的类别被预测为类2，但是从图中可以明显的看出待分类样本离类别1的点更近、更应该将其归为类1，为了处理这种情况，可以采用距离加权的方式，距离越近的点赋予其更大的权值。权值的计算方式有多种，这里介绍一种常用的方式——采用高斯函数计算权值。

       高斯函数的定义形式为

                                                                                   

      其中表示曲线的高度，表示曲线中心的偏移，表示半峰宽度（函数峰值一半处两点相距宽度），高斯函数的曲线图形大致为

                                         ​

    值可以设为1，值可以为0，值可以采用交叉验证法选择合适的值，在距离为0时，权值为1，距离越远，则权值越小，但不会为0。计算出个最邻近数据的权重后，待分类数据的类别与第  个数据的类别相同的概率为

                                                                                    

式中表示第  个数据的权值，将邻近的数据中属于同一类的数据的权值求和，那个类别上权值最大，就将待分类数据的类别定为该类。

4.K最邻近分类方法的优缺点

   4.1 优点

•  无需参数估计，无需训练，属于消极学习方法
•  对个别异常值不敏感，当然，前提时值不能过小
• 由于KNN方法主要靠周围有限的邻近的样本，而不是靠判别类域的方法来确定所属类别的，因此对于类域的交叉或重叠较多的待分样本集来说，KNN方法较其他方法更为适合

  4.2  缺点

•  计算复杂度高，涉及到距离的计算机排序操作
• 采用树建立模型需要消耗大量内存，尤其是在数据样本量大时
• 类别预测数据慢
• 仅适用于数据样本大的情况，数据样本量小时容易误分类