基于规则的分类技术

基于规则的分类技术
基于规则的分类是一种比较简单的分类技术，下面从以下几个方面对其进行介绍

1.任务

所有的分类技术的任务都是利用数据集训练出分类器，然后为每条记录贴上标签，对其进行分类，基于规则的分类任务也是如此。

2.结构

基于规则的分类使用了一组 $"if...then..."$ 的规则来对记录进行分类，其将这些规则组合起来，形成了如下所示结构

从上之下，当前规则去匹配记录，若当前规则与记录不匹配，则用下一条规则去匹配，直至找到能匹配的规则或者规则用完，结束分类过程。规则所处的位置可以用秩来表示，第一条规则秩最高，最后一条规则秩最低。

每一个分类规则可以表示为如下形式

$r_{i}:(c_{i}) ightarrow y_{i}$

$c_{i}$ 称为规则前件( $rule: antecedent$ )或前提( $precondition$ )，规则前件是属性测试的集合

$c_{i}=(A_{1}; op; v_{1})wedge (A_{2}; op; v_{2})wedge...wedge(A_{i}; op; v_{i})$

$(A_{i},v_{i})$ 为（属性，值）对， $op$ 为比较运算符，取自集合 $left { =, otequiv,<,>,leqslant ,geqslant ight }$ ， $y_{i}$ 为分类标签，称为规则后件。当规则 $r$ 的规则前件与记录 $x$ 的属性匹配时，则称 $r$ 覆盖 $x$ ；当 $r$ 覆盖某条记录时，则称规则 $r$ 被触发。

3.评分函数

基于规则的分类器的分类质量可以用覆盖率(coverage)和准确率(accuracy)来度量，二者的定义分别为
- 覆盖率：触发了规则的记录在数据集D中所占的比例
- 准确率：在触发了规则的记录中，分类正确的记录所占比例
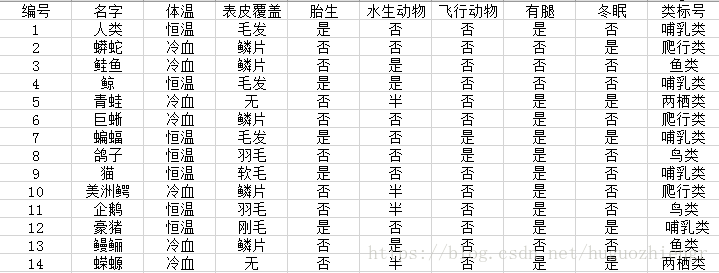
举个例子对覆盖率和准确率的定义进行说明，在脊椎动物的分类中，现有规则

（胎生=是）^（体温=恒温） $ightarrow$ 哺乳类

数据集D为

在以上14条记录中，记录1、4、7、9、12触发了规则，这5条记录的分类全部正确，该分类器的覆盖率及正确率分别为

$Coverage(r)=frac{5}{14}=0.357$

$Accuracy(r)=frac{5}{5}=1$

4.搜索、优化方法

4.1规则集的性质

在基于规则的分类器中，规则必须满足以下两条重要性质
- 规则互斥：一条记录不能触发两条及两条以上规则
- 规则穷举：数据集中每一条记录都能被规则覆盖
实现规则互斥，可以采用有序规则和无序规则两种方案。在有序规则方案中，规则集中的规则按照优先级降序排列，由覆盖记录的最高秩规则对记录分类，这样就避免多条规则间对记录分类的冲突。有序的规则集也称为决策表，第2节中介绍的分类器结构就是用的有序规则；在无序规则方案中，允许一条记录触发多条规则，规则被触发时视为对其相应类的一次投票，然后计算不同类的票数（可以使用加权方式）来决定记录的类所属。

基于有序规则的分类器对规则排序非常敏感，但是对记录分类时比较容易，不必把记录与每一条规则的前件进行比较，而基于无序规则的分类器则正好相反。在应用中计算量是一个需要重要点考虑的问题，因此一般基于规则的分类器采用有序规则。

在有序规则中，规则的排序有两种方案，一是基于规则的排序方案，二是基于类的排序方案。

4.2规则的排序

在基于规则的排序方案中，依据规则质量的某种度量（比如整体分类正确率等，具体的度量方式在不同的基于规则分类算法中会有所不同）对规则排序，这种排序方式确保每一个测试记录都由覆盖它的“最好的”规则来分类，这种分类方式能使得分类器的某种性能（即选择的规则质量的某种度量）达到最好，但是对于秩较低的规则，则不容易解释，因为它必须不满足秩高于它的规则中的至少一个（属性，值）。

在基于类的排序方案中，属于同一个类的规则放在一起，然后按照对“类”排序的方式对这些规则进行排序，同一个类中的规则相互间的顺序并不重要。这种排序方式使得每一条规则解释起来相对容易，但是可能存在质量较差的规则（即不能正确决定记录的类型）由于其所属类的秩较高，导致其秩也较高，造成误分类。

大多数著名的基于规则的分类器（如C4.5规则和RIPPER算法）都采用基于类的排序方案，因此下文中介绍的建立分类器的过程，都是基于类的排序方案。

4.3规则的提取算法

建立分类器的过程就是建立一套规则集，提取分类规则的方法有两类：(1)直接法，直接从数据集中提取分类规则 (2)间接法，从其他的分类模型（如决策树和神经网络）中提取分类规则，本文只说明使用直接法提取规则的过程。

顺序覆盖法(sequential covering)算法经常被用来直接从数据中提取规则，该算法每次提取一个类的规则，完成一个类的规则提取后再进行下一个类的规则提取。哪个类优先提取规则需要依据一定的原则，例如依据类包含的记录比例，比例高的类优先提取规则，或者依据类中记录的误分类率高低等，此处类规则提取顺序对应着4.2节中提到的类排序问题。顺序覆盖法的大致过程为：选择一个类 $c$ ，数据集中属于类 $c$ 的记录称为正例，否则称为反例，从数据集中学习出一条规则 $r$ ，如果规则 $r$ 覆盖大多数正例、没有或极少数反例，则认为规则 $r$ 可取，并添加到规则集 $R$ 中。当然，这里规则 $r$ 覆盖多少正例、反例才是可取的需要使用某种度量来决定，后面会介绍。该算法步骤如下
- 令E为训练记录，E中(属性，值)集合 $A=left { (A_{1},v_{1}),(A_{2},v_{2}),...,(A_{k},v_{k}) ight }$ ，类集合 $Y=left { y_{1},y_{2},...,y_{k} ight }$
- 令 $R=left { ight }$ 为初始规则列表，
- for ，表示空
  - while 终止条件不满足
    
    $r=leftarrow LearnOneRule(E,A,y)$
    
    $E=E-E_{r}$ ， $E_{r}$ 为 $r$ 覆盖的记录
    
    $Rleftarrow Rvee r$ ，添加 $r$ 到 $R$ 末尾
  - End While
- End for
在该算法中，while循环内的终止条件不唯一，在不同的分类器中可能会有区别，比如可以是所有整理均被覆盖，也可以是剩余正例比例小于某个阈值等。下面说明了顺序覆盖算法提取一个类中规则 $r1$ 和 $r2$ 的过程，在该过程中，每次提取一个规则之后，就将改规则覆盖的记录（包括正例和反例）去掉，并且对于每个类中的每条规则，都是从完整的（属性，值） $A$ 中提取。



在上述算法中， $LearnOneRule(E,A,y)$ 函数的作用是依据训练集 $E$ 、(属性，值)集合 $A$ 以及当前选中的类 $y$ 生成一条分类规则，最先想到的方法可能是将 $A$ 中包含的(属性，值)进行任意组合，形成规则，然后观察不同规则覆盖的正例和反例数，挑选符合要求的规则作为类 $y$ 的分类规则，但是这种方法的搜索空间是指数级的（ $A$ 中包含(属性，值)个数为 $p$ ，则其组合有 $p2^{p-1}$ 种），这在集合 $A$ 和训练集 $E$ 比较庞大时计算难度是爆炸的，因此在实际应用中， $LearnOneRule(E,A,y)$ 函数中规则生成策略一般有两种：从一般到特殊、从特殊到一般。

4.4规则生成策略

4.4.1 从一般到特殊

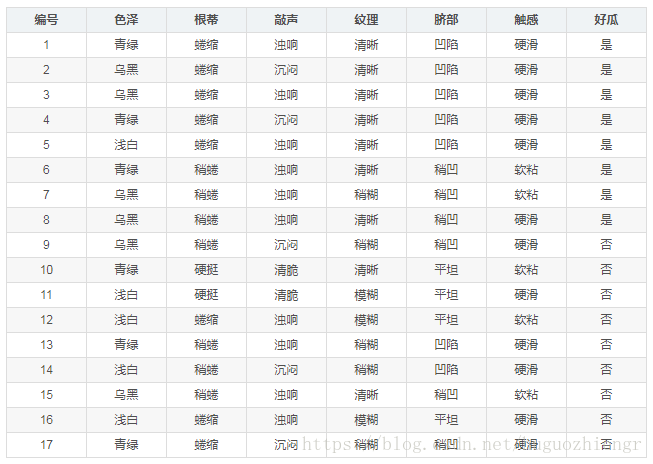
在该策略中，初始时规则 $r$ 前件为空，然后逐次的添加(属性，值)对，满足一定条件时停止添加(属性，值)对，生成一条规则，这个过程要考虑两个问题：(1)(属性，值)添加（选择）时的评估度量，决定(属性，值)添加顺序；(2)(属性，值)添加的终止条件。(属性，值)对的评估度量有多种，此处先以使用最简单的一种度量——准确率（规则覆盖的记录中被正确分类的比例）来说明规则生成策略，具体的度量在后面介绍。(属性，值)对添加的终止条件有三个：(1)添加(属性，值)后度量性能不提升；(2)类中正例已被全部覆盖，这实际上是条件(1)中的一种；(3)集合 $A$ 中(属性，值)已添加完，需要注意的是这里的终止条件与4.3节提到的算法中while循环的终止条件的区别。下面举例说明从一般到特殊的规则生成策略，现需要依据西瓜的特征来判断西瓜是好瓜还是坏瓜，训练记录如下



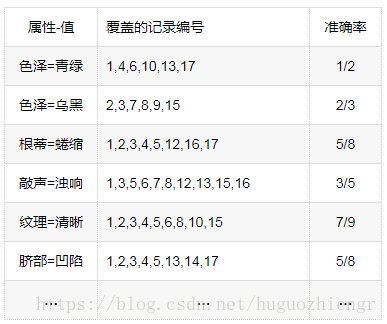
规则 $r$ 后件为（好瓜=是），前件从空开始，先添加第一个(属性，值)，候选(属性，值)、覆盖的部分记录编号及它的分类正确率分别如下



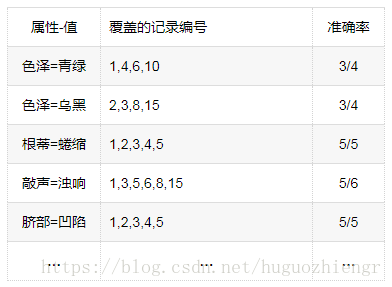
可以看到，(纹理=清晰)的正确率最高，因此首先在规则 $r$ 的前件中添加(纹理=清晰)，接着在(纹理=清晰)覆盖的记录中，继续规则 $r$ 前件中(属性，值)添加，候选的部分记录编号及它的分类正确率分别如下



在(纹理=清晰)覆盖的记录中，(根蒂=蜷缩)与(脐部=凹陷)覆盖记录的正确率都达到了100%，可以任选一个(属性，值)，这里可以选择(根蒂=蜷缩)（当出现这种情况时，可依据具体的任务和情况来考虑选择哪个，比如先考虑准确率，若准确率相同可以考虑覆盖率，若覆盖率相同则可以考虑属性出现的先后等），此时也达到了(属性，值)添加的终止条件，故在类(好瓜=是)中， $LearnOneRule(E,A,y)$ 函数生成了第一条规则

{(纹理=清晰)^(根蒂=蜷缩)} $ightarrow$ (好瓜=是)

接下来按照4.3节中的顺序覆盖算法，可以继续在类(好瓜=是)中生成规则。在顺序覆盖算法中，每次生成一条规则后，需要去掉该规则覆盖的记录，然后用新的记录集去生成下一条规则，而经常出现的情况是前后两条规则覆盖的记录实际上是有重合的，从一般到特殊的规则生成策略中，每次只考虑一个最优的(属性，值)，这显得过于贪心，容易陷入局部最优麻烦，为了缓解该问题，可以采用一种“集束搜索(beam search)”的方式，具体做法为：每次选择添加的(属性，值)时，可以保留前 $k$ 个最优的(属性，值)，而不是只选择最优的那个，然后对这 $k$ 个最优的(属性，值)继续进行下一轮的(属性，值)添加。

4.4.2 从特殊到一般

这种策略是从比较特殊的规则开始，逐渐删除(属性，值)，满足(属性，值)删除的终止条件：(1)删除(属性，值)后度量性能不提升；(2)类中正例已被全部覆盖，这实际上是条件(1)中的一种；(3)(属性，值)只剩下一个，规则生成的过程与4.4.1中类似。

从一般到特殊的策略更容易构建泛化性能比较好的分类器，且对噪声的鲁棒性更强，因此在一般的规则学习中通常采用该策略。从特殊到一般的策略适用于样本比较少的情况，在一阶规则学习这类假设空间比较复杂的任务上使用较多。

   4.5规则评估

在4.4.1中提到了(属性，值)添加（选择）时的评估度量，用了“正确率”度量，然而把正确率作为一个度量标准有一个潜在的局限性是没有考虑规则的覆盖率，例如考虑一个训练集，它包含60个正例和100个反例，现有两个候选规则

$r1:$ 覆盖50个正例和5个反例

$r2:$ 覆盖2个正例和0个反例

$r1$ 和 $r2$ 的正确率分别为90.9%、100%，然而 $r1$ 是较好的规则，尽管其准确率较低， $r2$ 的覆盖率太低了，其高准确率可能是噪声影响，具有潜在的欺骗性，以下几种度量标准可以处理这个问题

4.5.1 似然比统计量

构造如下似然比统计量 $LRS$

   $LRS=2 sum_{i=1}^{k}f_{i}log_{2}(f_{i}/e_{i})$

$k$ : 规则覆盖样例中包含类的个数

   $f_{i}$ : 属于类 $i$ 的样本的观测频率(类 $i$ 中包含的样例个数)

   $e_{i}$ : 在数据集中，规则做随机猜测的期望频率

在规则生成过程中，可以简单认为 $k$ =2，只有正例和反例两种， $e_{i}$ 也可以简单的理解为记录集中包含正例和反例的比例，较大的 $R$ 值表明做出正确预测数显著大于随机猜测的频率。在上面的例子中

   对规则 $r_{1}$

$f_{+}=50,f_{-}=5$ , $e_{+}=55 imes 60/100=20.625$ , $e_{-}=55 imes 100/160=34.375$

   $LRS(r_{1})=2 imes left [ 50 imes log_{2}(50/20.625)+5 imes log_{2}(5/34.375) ight ]=99.99$

   对规则 $r_{2}$

   $f_{+}=2,f_{-}=0,e_{+}=2 imes 60/100=0.75,e_{-}=2 imes 100/160$

   $LRSleft (r_{2} ight )=2 imes left [ 2 imes log_{2}(2/0.75)+0 imes log_{2}(0/0.125) ight ]=5.66$

   结果显示规则 $r_{1}$ 比 $r_{2}$ 好

   4.5.2 Laplace参数，m估计参数

Laplace参数考虑了规则的覆盖率，其定义为

   $Laplace=frac{f_{+}+1}{n+k}$

$m=frac{f_{+}+kp_{+}}{n+k}$

$n$ :规则覆盖的样例数

$f_{+}$ :规则覆盖的正例数

$k$ :类的总数

   $p_{+}$ :正类的先验概率

先验概率 $p_{+}=1/k$ 时，二者即相同。当覆盖率很低或n=0时，两个度量都接近于先验概率，而当覆盖率很高时，二者则接近于规则的准确率 $f_{+}/n$ 。在上面的例子中，

   $Laplace(r_{1})=frac{50+1}{55+2}=0.8947$

   $Laplace(r_{2})=frac{2+1}{2+2}=0.75$

结果显示规则 $r_{1}$ 比 $r_{2}$ 好

4.5.2 FOIL信息增益

假设规则 $r:A ightarrow$ 覆盖 $p_{0}$ 个正例和 $n_{0}$ 个反例，增加新的合取项 $B$ 后，扩展的规则 $r:B ightarrow$ 覆盖 $p_{1}$ 个正例和 $n_{1}$ 个反例，此时扩展规则后FOIL信息增益定义为

$FOIL=p_{1} imes left [ log_{2} frac{p_{1}}{p_{1}+n_{1}}-log_{2}frac{p_{0}}{p_{0}+n_{0}} ight ]$

该度量与 $p_{1}$ 和 $p_{1}/(p_{1}+n_{1})$ 成正比，所以它更倾向于选择那些高支持度计数和高准确率的规则，上面的例子中，

   $FOIL(r_{1})=50 imes left [ log_{2}frac{50}{55}-log_{2}frac{60}{160} ight ]=63.87$

   $FOIL(r_{2})=2 imes left [ log_{2}frac{2}{2}-log_{2}frac{60}{160} ight ]=2.83$

结果显示规则 $r_{1}$ 比 $r_{2}$ 好

4.6 剪枝

和决策树分类一样，剪枝的作用是缓解过拟合情况，提高基于规则的分类器的泛化能力，剪枝策略同样分为预剪枝和后剪枝。

      预剪枝发生在规则的生成过程中，选定4.5小节中介绍的某个度量，然后设定一个阈值，当添加(属性，值)后度量的增加（或减少）的值不满足阈值要求时，即停止(属性，值)的添加。

      后剪枝中最常用的策略是“减错剪枝(Reduced Error Pruning，简称REP)”，其基本做法是：将样例集分为训练集和验证集，从训练集中学得规则集 $R$ 后进行多轮剪枝，在每一轮穷举所有可能的剪枝操作，包括删除某条规则、某条规则中的部分(属性，值)等，然后用验证集对剪枝后所有的候选规则集进行评估，保留最好的规则集进行下一轮剪枝，如此继续，直到无法通过剪枝提高规则集在验证集上的性能。REP剪枝方法通常比较有效，但是它针对整体规则集进行剪枝，复杂度太高了。

     IREP(Incremental REP)方法的提出较大的降低了后剪枝的复杂度，其做法为：将样例集分为训练集和验证集，在生成一条规则 $r$ 后，立即在验证集上对该规则进行剪枝，得到规则 $r^'$ ，用 $r^'$ 替换 $r$ ，这样的过程仅对单条规则进行剪枝，因此比REP更高效。

     REP和IREP剪枝方法中用的度量不局限于正确率，可以使用4.5节中合适的度量。

5 .基于规则的分类方法的特点
- 基于规则的分类通常被用来产生更易描述的模型，且其分类性能与决策树相当
- 适用于处理类别分布不平衡的情况
相关阅读:
1323. Maximum 69 Number
1217. Play with Chips
1296. Divide Array in Sets of K Consecutive Numbers
1288. Remove Covered Intervals
1290. Convert Binary Number in a Linked List to Integer
1295. Find Numbers with Even Number of Digits
1306. Jump Game III
1305. All Elements in Two Binary Search Trees
1304. Find N Unique Integers Sum up to Zero
浅谈 JSON.stringify 方法【转】
原文地址：https://www.cnblogs.com/hgz-dm/p/10885963.html

基于规则的分类技术

1.任务

2.结构

3.评分函数

4.搜索、优化方法

4.1规则集的性质

4.2规则的排序

4.3规则的提取算法

4.4规则生成策略

4.5规则评估

4.6 剪枝

5 .基于规则的分类方法的特点