B,
题意就是你可以一次购买k件衣服,然后你只需付款最贵的那件价格,问你可以最多买多少件。
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using ld = long double;
int main() {
int cntTest;
cin >> cntTest;
for (int test = 0; test < cntTest; test++) {
int n, p, k;
cin >> n >> p >> k;
int pref = 0;
int ans = 0;
vector<int> a(n);
for (int i = 0; i < n; i++) {
cin >> a[i];
}
sort(a.begin(), a.end());
for (int i = 0; i <= k; i++) {
int sum = pref;
if (sum > p) break;
int cnt = i;
for (int j = i + k - 1; j < n; j += k) {
if (sum + a[j] <= p) {
cnt += k;
sum += a[j];
} else {
break;
}
}
pref += a[i];
ans = max(ans, cnt);
}
cout << ans << "
";
}
}
D.Enchanted Artifact
题意:一个密码锁,密码为长度<=300的,由a和b组成的字符串。每次你输入密码会返回一个耐久,耐久为最小删除/插入/修改的次数使得你输入的密码和答案相同的次数。给你n+2次机会尝试。n不知道。
题意:首先求出a和b的个数,方法是用300的a和300的b去试,那么a的个数就是300-c1,b的个数就是300-c2。那么len=c1+c2。之后c2表示还缺的b的个数。以len个a的字符串为基准开始试,每次修改一位为b。如果答案比c2小,说明改对了,这位就是b,--c2。如果答案比c2大,说明改错了,这位是a,就改回去,c2不变。最后一共用了n+2次。
#include<bits/stdc++.h>
using namespace std;
const int M=300;
int main(){
string s=string(M,'a');
int c1,c2;
cout<<s<<endl;cout.flush();
scanf("%d",&c1);
c1=300-c1;
s=string(M,'b');
cout<<s<<endl;cout.flush();
scanf("%d",&c2);
c2=300-c2;
if (c1==0){
s=string(c2,'b');
cout<<s<<endl;cout.flush();
scanf("%d",&c2);
return 0;
}
else if (c2==0){
s=string(c1,'a');
cout<<s<<endl;cout.flush();
scanf("%d",&c1);
return 0;
}
int len=c1+c2;
s=string(len,'a');
int c=0;
for(int i=0;i<len-1;++i){
s[i]='b';
cout<<s<<endl;cout.flush();
scanf("%d",&c);
if (c==0)
return 0;
if (c>c2)
s[i]='a';
else
--c2;
}
if(c2)
s[len-1]='b';
cout<<s<<endl;cout.flush();
scanf("%d",&c);
return 0;
}
C,就是给你,每个题有0,1,表示容易困难,每道题都有一直t值,表示如果你做题的时间大于等于tt,那你就必须把t值小于等于tt的题做完,你要做出最多的题目数。
思路就是,我们先给时间从小到大排序一个遍,然后接下来我们就可以进行比较,例如现在处理了i题,已经把时间计算好,再算到i+1的时间可以做几道简单题,这里可以先预先后缀和记录下。
#include <bits/stdc++.h>
using namespace std;
#define mem(a,b) memset(a,b,sizeof(a))
#define cin(a) scanf("%d",&a)
#define pii pair<int,int>
#define ll long long
#define gcd __gcd
const int inf = 0x3f3f3f3f;
const int maxn = 200100;
const int M = 1e9+7;
int n,m,k,t,x,y;
ll sum[maxn];
struct node
{
ll ty,t;
}a[maxn];
bool cmp(node a,node b)
{
return a.t < b.t;
}
int main()
{
cin(t);
while(t--)
{
cin(n);cin(m);cin(x);cin(y);
for(int i = 0; i < n; i++)
{
cin>>a[i].ty;
}
for(int i = 0; i < n; i++)
{
cin>>a[i].t;
}
sort(a,a+n,cmp);
a[n].t = m+1;
ll time = 0;
int res = 0;
for(int i = n-1; i >= 0; i--)
{
sum[i] = res; //求出i题后面有多少个简单题(不包括i)
if(a[i].ty == 0) res++;
}
int ans = 0;
if(a[0].t) ans=min((a[0].t-1)/x,sum[0]); //在t[0]前面做题
res=0;
for(int i = 0; i < n; i++)
{
if(a[i].ty==0) time+=x;
else time+=y;
if(time<a[i+1].t)
{
res=i+1;
res+=min((a[i+1].t-time-1)/x,sum[i]);
ans = max(ans,res);
}
}
cout<<ans<<endl;
}
return 0;
}
E
输入一个n,给出n-2个三角形。然后把他们拼成一个多边形,多边形的序号和三角形的序号对应,可以是乱序。输出两个东西,一个是三角形的序号,可以随便以哪个序号开头都可以,第二个东西就是我们按照那种顺序拿。
例如下面:
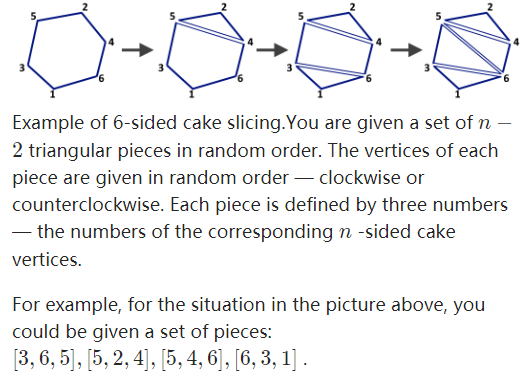
对于第一个问题我们可知道,求出的顶点也就是形成外边的,也就是只用一次的边,所以我们需要的就是记录只用一次的边的顶点,所以我们这里想到了异或,让和这个顶点相连接的每个顶点都和他异或一下,例如上图2连接着5和4两个点,故我们可令e【2】^=5,e【2】^=4,这样一个点如果知道另外一个点就可以通过异或还原出另一个点,所以我们需要的操作就是将每条边用map记录他用几次,
后面我们随便找出一条用了一次的一条边,就可以找到两个点,接着就可以由两个点得出其他店。
对于第二个问题,我们知道每个三角形都是一刀切出两个,也就是切的一刀的这条边共用两个三角形,故我们发现一条边用了两次,就将这两个三角形建无向边,再后续dfs输出就行
#include<bits/stdc++.h>
using namespace std;
map<pair<int,int> , vector<int> > m;
const int N=1e5+7;
vector<int> p[N];
int n,e[N];
void init()
{
for(int i=0;i<=n+1;i++) p[i].clear(),e[i]=0;
m.clear();
}
void dfs(int u,int f){
// cout<<"---"<<u<<endl;
// cout<<u<<' ';
for(int i=0;i<p[u].size();i++){
if(p[u][i]==f) continue;
dfs(p[u][i],u);
}
printf("%d ",u);
}
int main()
{
int t ; cin>>t;
while(t--){
scanf("%d",&n);
init();
for(int i=1;i<=n-2;i++){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
if(a>b) swap(a,b);
if(b>c) swap(b,c);
if(a>b) swap(a,b);
e[a]^=b,e[a]^=c;
e[b]^=a,e[b]^=c;
e[c]^=b,e[c]^=a;
m[{a,b}].push_back(i);
m[{b,c}].push_back(i);
m[{a,c}].push_back(i);
}
int x,y;
for(auto u:m){
if(u.second.size()==1){
x=u.first.first;
y=u.first.second;
break;
}
}
printf("%d %d ",x,y);
for(int i=1 ;i<=n-2;i++,swap(x,y)) printf("%d ",(x^=e[y]));
for(auto u:m){
if(u.second.size()==2){
p[u.second[0]].push_back(u.second[1]);
p[u.second[1]].push_back(u.second[0]);
}
}
puts("");
// cout<<"----"<<endl;
dfs(1,0);
printf("
");
}
}