B
定n,m,长度为n的数组a,长度为n的数组b
所有a[i]加上x后再对m取余,使得a[i]与b[i]相等(与顺序无关),保证有解,输出最小的非负x
其实我们知道就是,这个序列加x模m,实际上就是,找出a序列后面再加上自己,找出某个位置为起点的序列,这个序列的等差等于b的差值序列,所以我们只需给后面那串a加上m,然后求出自己差值序列,进行kmp匹配,由于我们已经进行排序,找到的第一个必是最小的。
最后防止是复制就要+m%m
#include<bits/stdc++.h>
using namespace std;
const int mod=1e9+7;
const int maxn=5e3+10;
int a[maxn],pre[maxn],b[maxn],pre2[maxn],n,m;
int Next[maxn];
void get_Next()
{
for(int i=1;i<n-1;i++)
{
int j=Next[i];
while(j&&pre2[i]!=pre2[j])j=Next[j];
Next[i+1]=pre2[i]==pre2[j]?j+1:0;
}
}
int kmp()
{
get_Next();
int j=0;
for(int i=0;i<2*n-1;i++)
{
while(j&&pre[i]!=pre2[j])j=Next[j];
if(pre[i]==pre2[j])j++;
if(j==n-1)return i-(n-1)+1;
}
return -1;
}
int main()
{
cin>>n>>m;
for(int i=0;i<n;i++)cin>>a[i];
for(int i=0;i<n;i++)cin>>b[i];
sort(a,a+n);
sort(b,b+n);
for(int i=n;i<2*n;i++)a[i]=a[i-n]+m;
for(int i=1;i<2*n;i++)pre[i-1]=a[i]-a[i-1];
for(int i=1;i<n;i++)pre2[i-1]=b[i]-b[i-1];
int ans=kmp();
cout<<(b[0]+m-a[ans]+m)%m<<endl;//两个m
return 0;
}
c是构造题,给你一个数字n,你要求出最小的大于n的数字,而且这个数字必须满足bi=b(i+k),例如(k=2)15151。
是一个构造题,我们先不考虑各种情况,给你一个5位的数字,例如12345,k=2,那么可以直接将将0~k-1位置的数字不断重复就行,12121,但是题目要求最小大于的n,所以构造就得考虑了,我们知道ni和n(i+k)的关系要么想等没事,要么大于要么小于,当你大于的时候直接构造没啥事,但是你小于直接构造那就构造出小于n的了,所以找出第一个位值,这个位置(pos+k),使得n(pos)小于n(pos+k),那么我们直接将n(pos)+1然后后面的值到k-1位置赋值为0,就行了,这个很简单就想出来,但是,我们还忽略一个状况,没错在pos+k这个位置之前有一个位置x+k,被n(x)给增大了,即n(x)大于n(x+k),那么n(x+k)被增大了后面小于大于都无所谓了,所以我们还得判断第一个n(x)>n(x+k)的最小的x+k和最小的n(y)<n(y+k)的最小y+k进行比较
话说这个string好方便,可以直接++。。。。。
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/pb_ds/detail/standard_policies.hpp>
using namespace std;
using namespace __gnu_pbds;
#define SZ(x) ((int)(x).size())
typedef long long ll;
typedef pair<int, int> pii;
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> ordered_set;
const int N = 2e5 + 5;
const int OO = (int) 2e9;
int n, k;
string a;
char r[N];
int iss[N];
bool up[N];
void print() {
string res;
for (int i = 0; i < n; i++) {
res += r[i % k];
}
cout << n << endl;
cout << res << endl;
}
int main() {
std::ios_base::sync_with_stdio(false), cin.tie(NULL), cout.tie(NULL);
cin >> n >> k >> a;
int mnUp = n, mnAdd = n;
bool flag = 0;
vector<int> v;
for (int i = 0; i < k; i++) {
r[i] = a[i];
for (int j = i + k; j < n; j += k) {
if (a[i] != a[j]) {
flag = 1;
iss[i] = j;
if(a[i] < a[j]) {
// mnUp = min(mnUp, j);
up[i] = 1;
v.push_back(j);
}
else if (a[i] > a[j]) {
mnAdd = min(mnAdd, j);
}
break;
}
}
}
if (!flag) {
cout << n << endl;
cout << a << endl;
return 0;
}
sort(v.begin(), v.end());
for (int i = k - 1; i >= 0; i--) {
if (SZ(v) && v[0] < mnAdd && a[i] != '9') {
r[i]++;
for (int j = i + 1; j < k; j++)
r[j] = '0';
print();
return 0;
}
}
print();
return 0;
}
D
给定n,给定长度为n的数组a,a[i]表示第i列的正方块的数量,i和a[i]都不大于3e5(掐指一算,遍历不行)
用1×2或者2×1的长方块填满图像,问最多能用几个
首先如果全都是偶数的就直接可以算出来了,但是有奇数,这时候贪心地发现奇数所空出来地一个,如果有第二个奇数列就可以连起来做出一个贡献如下(1)一样,但是我们发现这个奇数列位置得一奇一偶才可以贡献1,故我们奇数x++,偶数y++,res+=min(x,y);
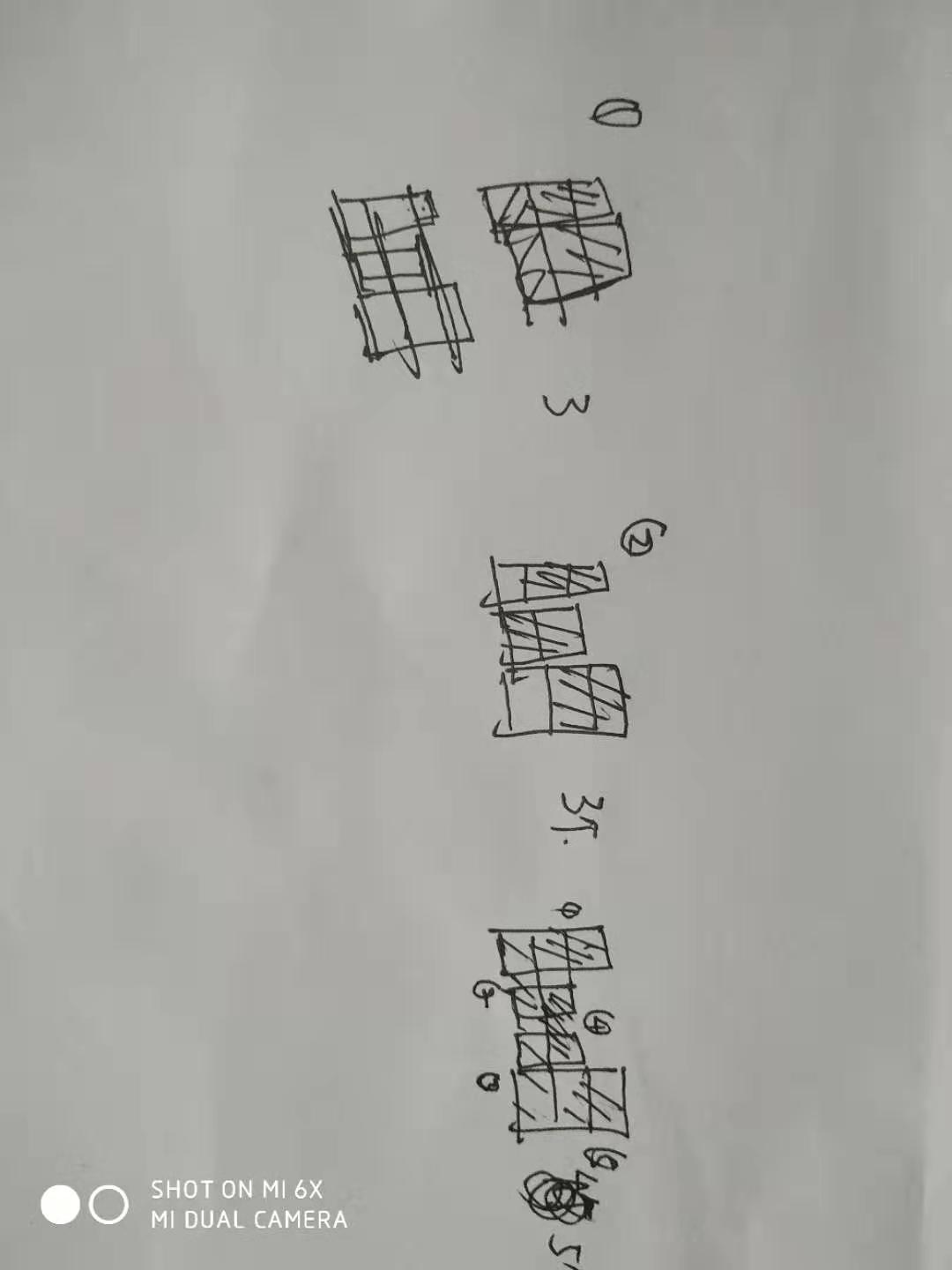
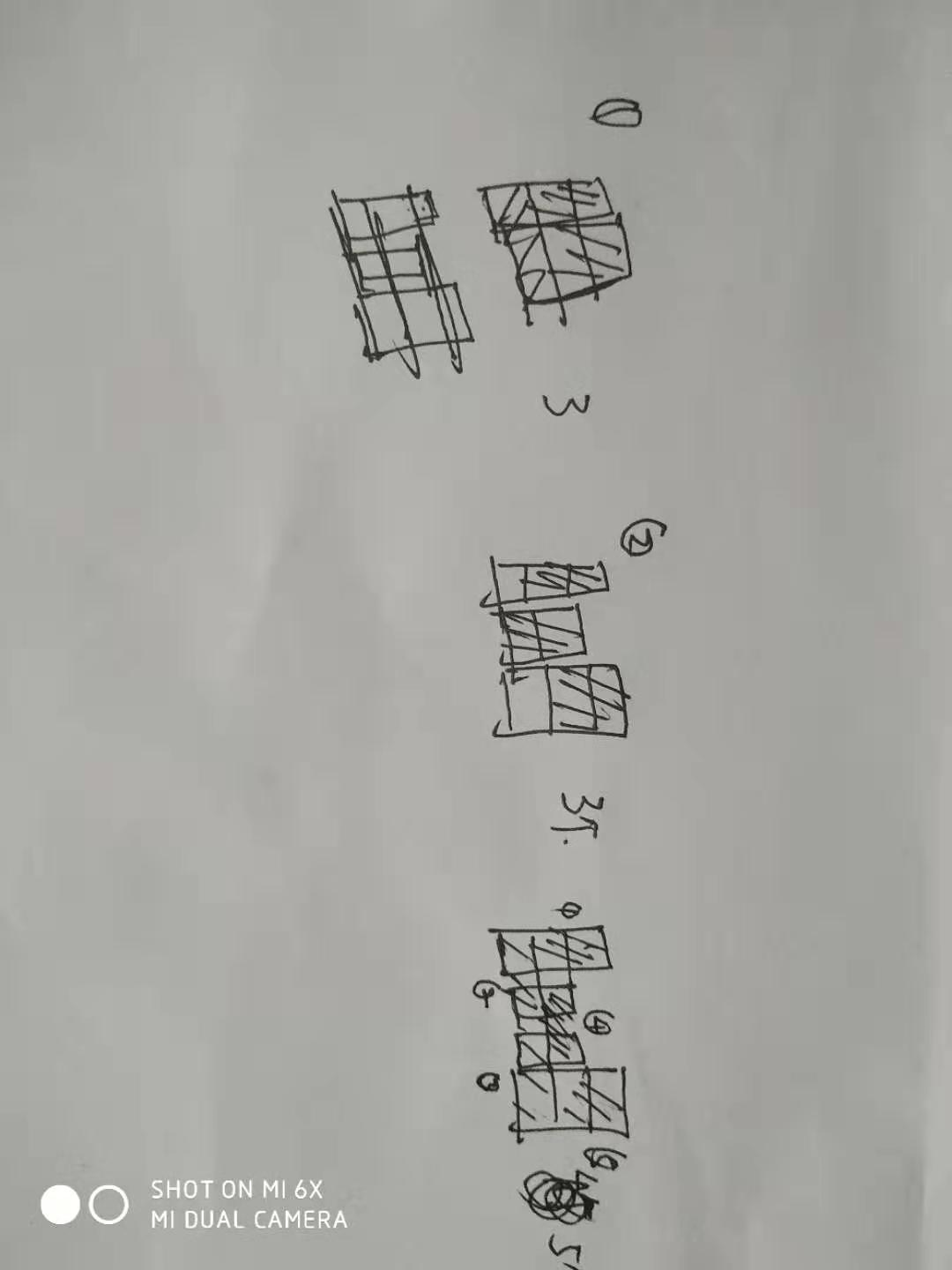
#include<bits/stdc++.h>
using namespace std;
int main()
{
long long res=0,x=0,y=0,n,m;
scanf("%lld",&n);
for(int i=1;i<=n;i++)
{
scanf("%lld",&m);
res+=m/2;
if(m&1)
{
if(i&1)x++;
else y++;
}
}
res+=min(x,y);
printf("%lld
",res);
return 0;
}