前缀、中缀、后缀表达式

1. 定义

对表达式的不同记法，区别在于 运算符相对操作数的位置：

1. 中缀：运算符在操作数中间：如(3 + 4) × 5 - 6。 人习惯的表达方式
2. 前缀：运算符在操作数之前：如- x + 3 4 5 6。 计算机方便操作的方式：从右至左数据入栈，遇到操作符，弹出栈顶两个数运算，并将结果入栈
3. 后缀：运算符在操作数之后：如3 4 + 5 x 6 -。计算机方便操作的方式：从左至右数据入栈，遇到操作符，弹出栈顶两个数运算，并将结果入栈

为了计算机处理方便，一般需要把中缀表达式转换为前缀表达式或后缀表达式处理；为了人看方便，一般需要把前缀和后缀转换为中缀表达式

2. 前缀和后缀转换为中缀表达式

方法一：采用String存储中缀表达式

同上边讲的计算机的操作过程一致，只不过可以采用String存储数据，原来的运算操作改为字符串重构操作，如对于前缀表达式，从右至左，遇到操作符“+”，则把栈顶的两个操作符弹出，重构字符串“（3+4）”入栈。

对于括号的处理，考虑操作符优先级，如果括号内的操作符优先级不比括号外操作符优先级低，就可以去掉括号。

 

方法二：采用树存储中缀表达式

如：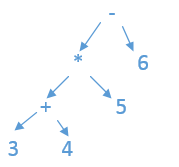

1.  前缀转中缀：正序遍历前缀表达式，遇到操作符，以操作符为树根，构建其左右子树；遇到数，查找右子树为空的祖先节点，构建为右孩子。采用递归+栈
2. 后缀转中缀：逆序遍历后缀表达式，遇到操作符，以操作符为树根，构建右左子树；遇到树，查找左子树为空的祖先节点，构建为左孩子。采用递归+栈

3. 中缀表达式转换为前缀或后缀表达式

方法一：加括号法

按照运算符优先级给所有未加括号的运算单位加括号，如( ( (3+4) * 5 ) - 6 )，

1. 中缀转前缀：把操作符移到对应括号前面，然后去掉括号。如 - ( * ( + (34) 5 ) 6 )  ------->   -*+3456 
2. 中缀转后缀：把操作符移到对应扩后后面，然后去掉括号。如 ( ( (34) + 5 ) * 6 ) - -------> 34+5*6-

 

方法二：采用树存储中缀表达式，则前序遍历就是前缀表达式，后序遍历就是后缀表达式

 

方法三：利用两个栈，操作符栈s2和中间结果栈s1实现转换

1. 中缀转前缀：从右至左遍历，遇到数字，push到栈s1；遇到操作符，如果s2.top()为空或者右括号，或者top比当前操作符优先级低或相等，则将操作符push到s2；否则，s2出栈；遇到括号，如果是右括号，入栈，如果是左括号，则将s2一直pop到s1，直到遇到一个右括号，这两个括号会被抛弃。 遍历结束后，把s2的剩余操作符依次push到s1。最后把s1的内容依次弹出，就是前缀表达式。--------原理：中缀表达式计算中，高优先级的先计算，同等优先级排在前面的先计算。前缀表达式计算是从右至左算，所以高优先级的排在靠右的地方，同等优先级排在前面的地方最终排在靠右的地方。如果以栈的形式来存储结果，那么高优先级和同等优先级排在前面的：在s1中先入栈（出栈后排在右边），在s2中后入栈，----->top比当前操作符优先级高，如果push到s2，则顺序不对了，即优先级高的在s2中先入栈，所以要先pop入栈s1（其中，同等优先级排在前面的在s2中后入栈，最后pop到s1则是先入栈）。    而括号内包含的算是一个整体，一个高优先级整体，所以遇到左括号这个整体完整了，因为优先级高，要尽快入栈s1-----如果是左括号，则pop到栈s1
2. 中缀转后缀：从左至右遍历，遇到数字，push到队列s1；遇到操作符，如果s2.top()为空或者左括号，或者比当前操作符优先级低，则将操作符push到s2；否则，s2出栈；遇到括号，如果是左括号，入栈，如果是右括号，则将s2一直pop到s1，直到遇到一个左括号，这两个括号会被抛弃。遍历结束后，把s2的剩余操作符依次push到s1。最后把队列s1的内容依次出队列，就是后缀表达式。--------原理：基本同上。前缀表达式是从从左至右算，高优先级的排在靠左的地方，同等优先级排在前面的地方最终也排在靠左的地方。 如果以队列形式存储结果，那么高优先级和同等优先级排在前面的：在s1中先入队列（出队列后排在左边），在s2中后入栈。---->top比当前操作符优先级高或相等，如果push到s2，则顺序不对，即高优先级和同等优先级排在前面的的在s2中先入栈，所以要pop到s1。  括号内包含一个高优先级整体，由于从左至右遍历，先出现左括号，遇到右括号，说明这个整体完整了，要尽快入队列s1------如果是右括号，pop到s1

参考：http://blog.csdn.net/antineutrino/article/details/6763722

http://blog.sina.com.cn/s/blog_4e0c21cc01010x38.html

http://blog.csdn.net/expleeve/article/details/7166521