1、定义
算法就是一系列的计算步骤,用来将输入数据转换为输出结果。
2、算法的共同特征
1)有很多候选的解决方案,其中大部分不是我们所需要的。
2)有着实际的应用。如最短路。
3、章节框架
1)伪代码描述 2)证明算法正确性(循环不变式) 3)时间效率分析
3.1 循环不变式
有三个性质:
1)初始化:它在循环的第一轮迭代开始之前,应该是正确的。
2)保持:如果在循环的某一次迭代开始之前它是正确的,那么,在下次迭代开始之前,它也应该保持正确。
3)终止:当循环结束时,不变式给了我们一个有用的性质,它有助于表明算法是正确的。
3.2 算法的时间分析
- 算法的运行时间:指在特定输入时,所执行的基本操作数(或步数)
- 一般我们考察算法的 最坏情况运行时间:
- 一个算法的最坏情况运行时间是在任何输入下运行时间的一个上界。即能确保算法的运行时间不会比这一时间更长。我们不需要对运行时间做某种复杂的猜测,并期望它不会变得更坏了。
- 对于某些算法来说,最坏情况出现得相当频繁。例如要找的信息不在数据库。
- 大致上看来,平均情况与最坏情况一样差。例如插入排序的平均情况运行时间和最坏情况下的运行时间都是输入规模n的一个二次函数
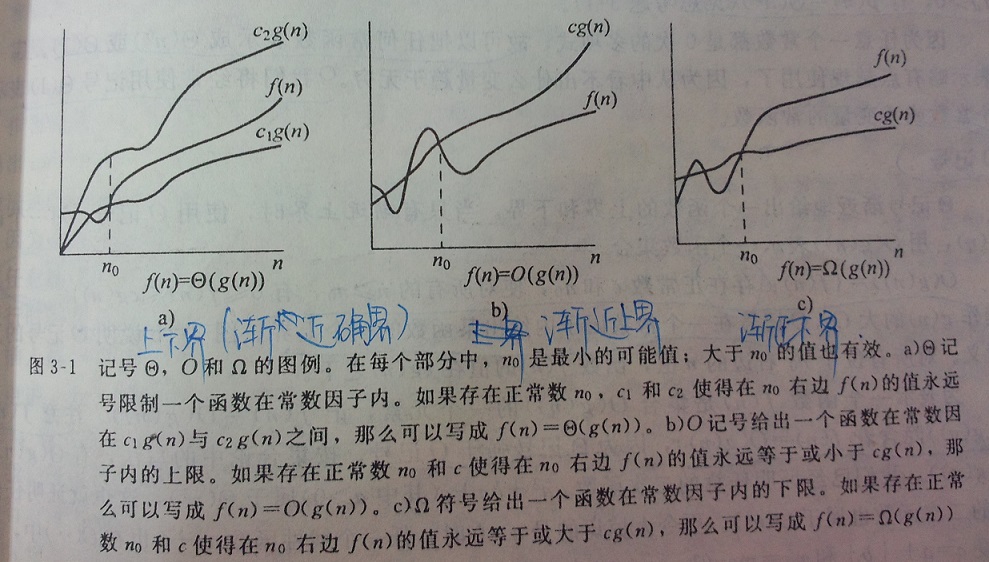
- 各种渐进符号:
- 渐进确界:Θ。Θ(g(n)) = {f(n): 存在正常数c1,c2,n0,使对所有的n≥n0,有0 ≤ c1g(n) ≤ f(n) ≤ c2g(n) }。即对任意一个函数,存在正常数c1,c2,当n充分大时,f(n)能被夹在c1g(n)和c2g(n)之间,则f(n)属于集合Θ(g(n)).
- 渐进下界:Ω。Ω(g(n)) = {f(n): 存在正常数c和n0,使对所有的n≥n0,有0 ≤ cg(n) ≤ f(n) }
- 渐进上界:O。O(g(n)) = {f(n): 存在正常数c和n0,使对所有的n≥n0,有0≤ f(n) ≤ cg(n) }
- 非渐进紧确的上界:ο。o(g(n)) = {f(n): 对任意正常数c,存在正常数n0,使对所有的n≥n0,有0≤ f(n) ≤ cg(n) }
- 非渐进紧确的下界:ω。ω(g(n)) = {f(n): 对任意正常数c,存在正常数n0,使对所有的n≥n0,有0 ≤ cg(n) ≤<f(n) }