【解释】

【解释】
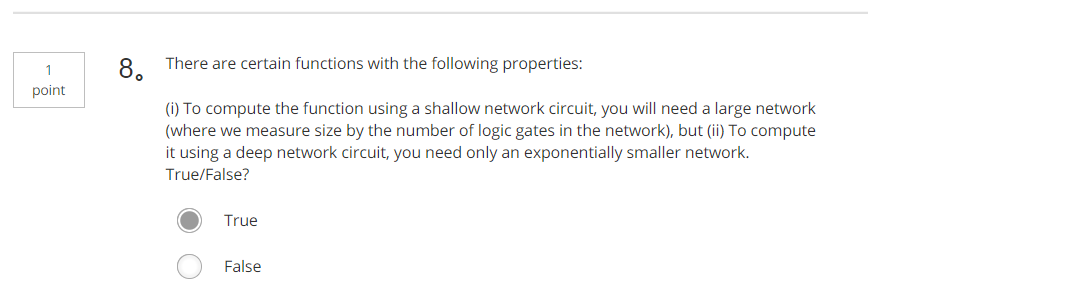
比如算法中的learing rateα(学习率)、iterations(梯度下降法循环的数量)、L(隐藏层数目)、n[l] (隐藏层单元数目)、choice of activation function(激活函数的选择)都需要你来设置,这些数字实际上控制了最后的参数W和b的值,所以它们被称作超参数。

【解释】
在深度神经网络的这许多隐藏层中,较早的前几层能学习一些低层次的简单特征,等到后几层,就能把简单的特征结合起来,去探测更加复杂的东西。比如你录在音频里的单词、词组或是句子,然后就能运行语音识别了。同时我们所计算的之前的几层,也就是相对简单的输入函数,比如图像单元的边缘什么的。到网络中的深层时,你实际上就能做很多复杂的事,比如探测面部或是探测单词、短语或是句子。

【解释】
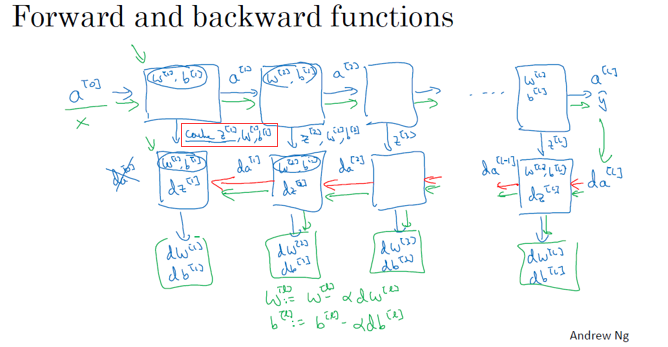
如果你回顾一下向量化的全过程,其实就是一个for循环,for循环 i从1到4,for循环 i等于1到大写L,然后你去计算第一层的激活函数,接着算第2、3、4层,所以看起来是个for循环。我猜你在用代码实现自己的网络时,通常是不想用显式for循环的,但是在这个情况下除了显式for循环,并没有更好的办法,所以当我们在实现正向传播的时候,用for循环也是可以的,它可以计算第一层的激活函数,然后按顺序算好第2、3、4层等等,应该没有人能用除了for循环以外更好的方法来一层层地计算1到L,也就是从输入层到输出层的整个神经网络,这个地方用显式for循环是可以的。



【解释】
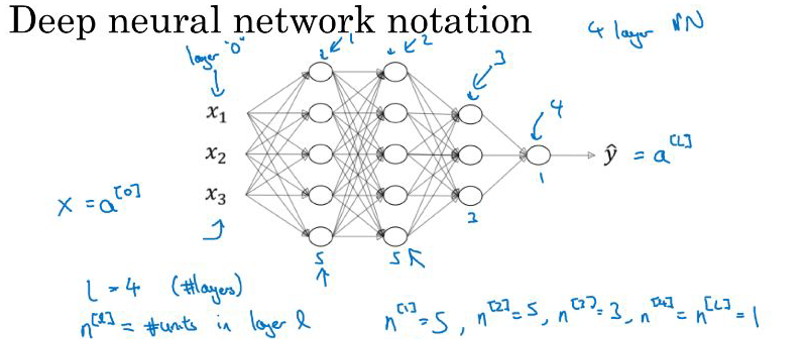
例如,上图是一个四层的神经网络,有三个隐藏层。我们用L表示层数。记住当我们算神经网络的层数时,我们不算输入层,我们只算隐藏层和输出层。
【解释】

反向传播过程中,计算需要用到g[l]的倒数,所以需要知道激活函数的什么。