一、什么是堆
如果一个完全二叉树的每个节点,都不大于它的子节点,就可以称之为堆。所谓完全二叉树,就是除了叶子节点以外,所有的其他节点,都有完整的左字树和右子树,除了最后一层的非叶子节点以外。

二、堆排序算法的大体脉络
1、对无序的数据先建一个堆,
2、输出堆顶元素,
3、然后以最后一个元素代替堆顶元素,
4、进行调整,使之仍然为一个堆。
5、重复步骤2,3,4,直到堆中只剩下一个元素。
三、堆排序算法的详细过程
1、填充
首先,将这些无序的数字,填充成一个完全二叉树,但这时一般是不能够满足堆的要求的。没有关系,我们后面来进行调整。先来看看填充的过程。实际上,填充的顺序就是按照树的层次遍历的顺序,即从上到下,从左到右,一层一层往下放。就这样放完一层,放二层,放完二层,放三层,直到所有的数都放完为止。
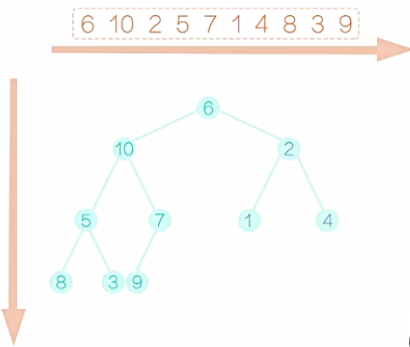
2、建堆
填充完毕后,开始建堆的过程。显然,所有的叶子节点,都满足建堆的要求,因为它没有字节点。我们可以从最后一个非叶子节点开始。如图1所示,这里就是7,它满足堆的要求,再向前看5,这个节点不满足要求,右字树比它要小,需要把它和右子树互换一下,互换后如图2所示。再向前看2,它需要和做孩子互换,互换后,如图3所示。再向前看,现在到10,和之前的情况有些不同,10比之前的两个孩子都大,那到底该和哪一个孩子交换呢?稍微考虑一下,我们应该和最小的那个孩子交换,不然的话,我们交换完以后,仍然不能满足堆的要求。换过后,如图4所示。注意,10 换下来以后,破坏了原来满足要求的字树,所以还应该再调整,10和5应该互换,互换后,如图5所示。最后是6和1换,换后如图6所示。注意,6换下来以后,破坏了原来满足要求的字树,所以还应该再调整,6和2应该互换,互换后,如图7所示。至此,一个堆就建好了。这个堆满足的性质是,所以的父节点的值都不大于它的叶子节点的值。
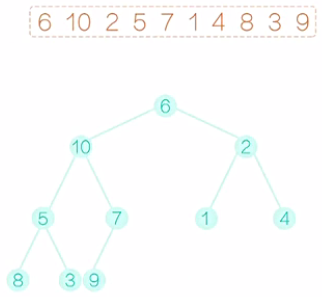

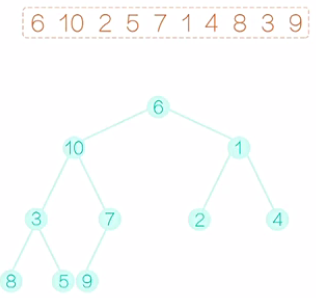
图1 图2 图3
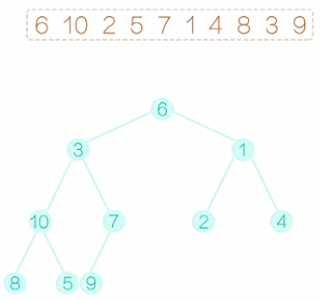
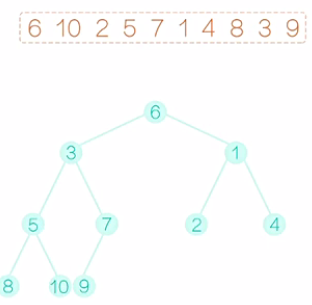
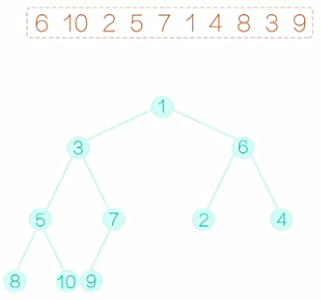
图4 图5 图6
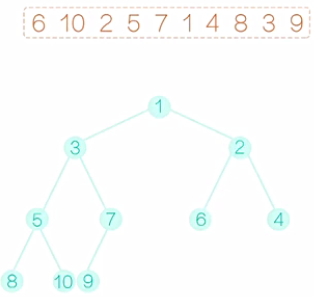
图7
3、筛选并输出堆顶元素
从初始的这个堆中,输出堆顶的这个元素。如图8所示,先输出1,然后根节点就空了。接着如图9,我们可以把最后一个元素9提拔上来,让9做根元素。显而易见,现在除了新提拔的这个根节点以外,其他的节点都满足堆的性质,那么就需要调整这个根节点。9要和左右孩子相比,与较小的孩子2互换。换后如图10所示。接着对局部的数,我们再调整,直到9落地为止,换后如图11。至此,这个完全二叉树就满足堆的要求了,我们输出2,如图12。然后,如图13,把最后一个元素10提拔上去,然后,还像之前一样,把10逐步向下调整,这个完全二叉树满足堆的要求后,输出堆顶的元素3,如图14。在堆排序的术语上,我们把较大的元素从顶层落到底层的过程称为“筛选”。然后再把最后一个元素提拔上去,在筛选,再提拔,再筛选,重复这个过程,堆变得越来越小,直至整个堆只剩下一个元素,把这个元素也输出,我们的堆排序过程也就结束了。
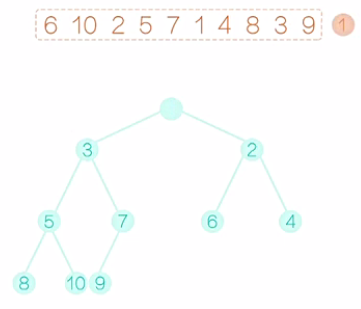
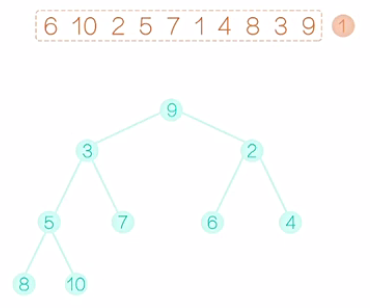

图8 图9 图10
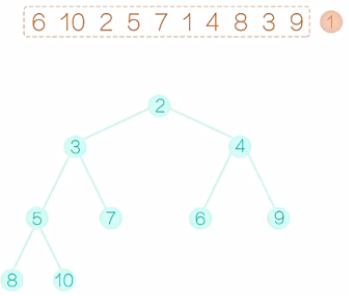
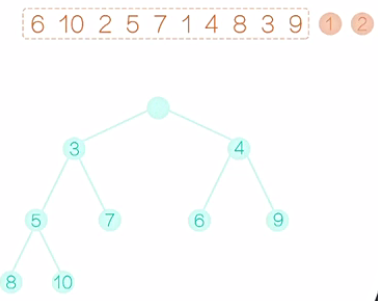
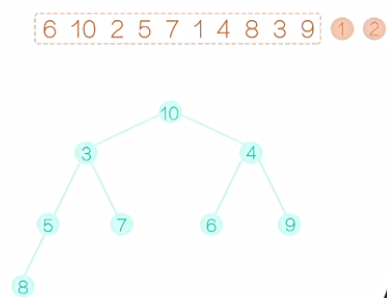
图11 图12 图13

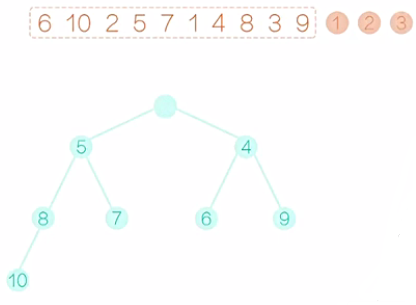
图14 图15
四、代码实现
堆排序可以用二叉树的结构来表示,但在 实际应用中,我们还可以更节省内存空间,用一位数组来表示这个二叉树,当数据量很大的时候,一维数组占用的内存比二叉树占用的内存小很多。当然,对于一般的二叉树,我们是不能这样表示的,现在的完全二叉树具有特殊性,我们可以用一维数组来表示它。
从面向对象的角度出发,对二叉树,这要能给点一个节点,确定父节点和子节点在哪里就可以了,至于在内存中怎么存储的,并不重要。如下图所示,对于完全二叉树,给定当前节点,其父子点和子节点都是可以唯一确定的。把这些节点序号,对应到一维数组元素的下标,就可以用一维数组来表示完全二叉树了。

因为我们用一维数组来代替完全二叉树,所以填充的过程就免去了,可以直接进行筛选,然后提拔最后一个元素,再筛选,直至堆中只剩下最后一个元素,输出,堆排序完成。代码如下:

public class HeapSort { public static void main(String[] args) { int[] a={7,2,3,6,8,5}; heapSort(a); } public static void heapSort(int[] a){ //建立初始堆 for(int i=(a.length-1)/2;i>=0;i--) heapOne(a,a.length,i); //边输出堆顶,边调整 int n=a.length; //剩余元素数 while (n>0){ System.out.print(a[0]+" ");//输出堆顶元素 a[0]=a[n-1];//最后一个元素移动到堆顶 n--;//要排序的数组的长度减1 heapOne(a,n,0); } System.out.println(); } //节点K进行筛选 //a:堆数据 , n:堆中有效数据的个数 ,K:待筛选的节点 public static void heapOne(int[] a,int n,int k){ int k1=2*k+1; //K节点的左子节点 int k2=2*k+2; //K节点的右子节点 if(k1>=n && k2>=n) return;//已经是叶子了 int a1=Integer.MAX_VALUE; int a2=Integer.MAX_VALUE; if(k1<n) a1=a[k1]; //左孩子值 if(k2<n) a2=a[k2]; //右孩子值 if(a[k]<=a1&&a[k]<=a2) return;//已经符合堆的要求了 //找到左右孩子中最小的,和它交换 if(a1<a2){ int t=a[k]; a[k]=a[k1]; a[k1]=t; heapOne(a,n,k1);//继续筛选子树 }else { int t=a[k]; a[k]=a[k2]; a[k2]=t; heapOne(a,n,k2);//继续筛选子树 } } }
------------------------------------------------------------------------------------------------------------------------------------------------
参考链接:
http://www.iqiyi.com/v_19rrhzzs1k.html
