Himmelblua函数在(-6,6),(-6,6)的二维平面上求极值
函数的数学表达式:f(x, y) = (x**2 + y -11)**2 + (x + y**2 -7)**2; 如下图所示
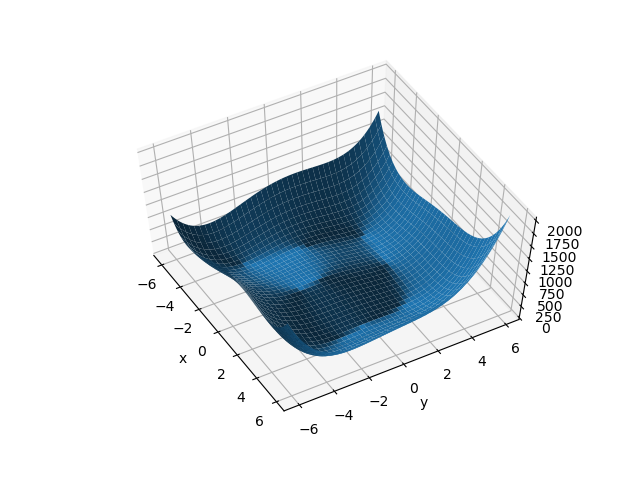
等高线如下图所示:
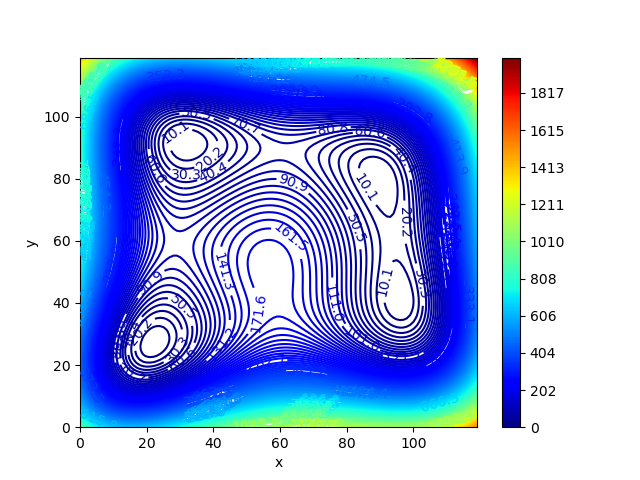
代码如下:
# encoding: utf-8 import tensorflow as tf import numpy as np import matplotlib.pyplot as plt import matplotlib as mpl from mpl_toolkits.mplot3d import Axes3D from mpl_toolkits.axes_grid1 import ImageGrid # Himmelblau function def himmelblua(x): return (x[0] ** 2 + x[1] - 11) ** 2 + (x[0] + x[1] ** 2 - 7) ** 2 # 产生三维数据 x = np.arange(-6, 6, 0.1) # 创建等差数组,步长为0.1 y = np.arange(-6, 6, 0.1) print('x, y range:', x.shape, y.shape) X, Y = np.meshgrid(x, y) print('X, Y maps:', X.shape, Y.shape) Z = himmelblua([X, Y]) max = np.max(Z) min = np.min(Z) # 画三维图 fig = plt.figure('himmelblua') ax = fig.gca(projection='3d') # 设置3D坐标轴 ax.plot_surface(X, Y, Z) # 3D曲面图 ax.view_init(60, -30) ax.set_xlabel('x') ax.set_ylabel('y') plt.show() # 画等高线图 N = np.arange(min, max, (max-min)/200) fig = plt.figure('contour') ct = plt.contour(Z, N, linewidth=2, cmap=mpl.cm.jet) # 计算等高差 plt.clabel(ct, inline=True, fmt='%1.1f', fontsize=10) plt.colorbar(ct) plt.xlabel('x') plt.ylabel('y') plt.savefig('contour-himmelblua.png') plt.show() # 初始化参数 x = tf.constant([4., 0.]) # 寻找极小值数值解 for step in range(200): with tf.GradientTape() as tape: tape.watch([x]) y = himmelblua(x) grads = tape.gradient(y, [x])[0] x -= 0.01*grads if step % 20 ==19: print('step {}: x={}, f(x)={}'.format(step, x.numpy(), y.numpy()))
经过迭代后的值越来越精确,这里就不表了!