【LG3783】[SDOI2017]天才黑客

【LG3783】[SDOI2017]天才黑客

题面

洛谷

题解

首先我们有一个非常显然的(O(m^2))算法，就是将每条边看成点，
然后将每个点的所有入边和出边暴力连边跑最短路，我们想办法优化这里的连边。

具体怎么做呢，我们将所有入边和出边在( ext{Trie})树上所对应的点放在一起按(dfs)序排一遍序，那么相邻两个点的距离就是(dep_{lca})，任意两点之间距离就是他们之间所有的(dep_{lca})取个(min)。

那么如何优化连边呢，我们考虑建如图所示的四排点：

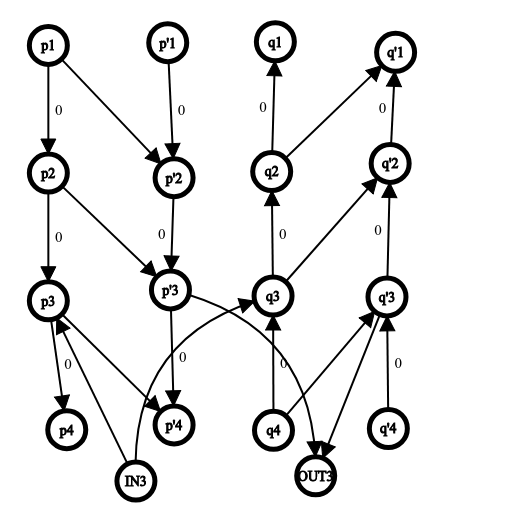
其中(p)号节点从(dfs)序小的往大的连(0)边，(q)号点反之。
然后相邻的(p)和(p')之间连他们两两之间的(dep_{lca})，(q)点亦然。

然后入点向编号对应的(p,q)连(0)边，(p',q')向出点连(0)边，然后发现两点之间的距离都可以取(min)啦，这样子我们就可以直接跑(dijkstra)即可。
(具体实现详见代码)

代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring> 
#include <cmath> 
#include <algorithm>
#include <vector>
#include <queue> 
using namespace std; 
inline int gi() {
    register int data = 0, w = 1;
    register char ch = 0;
    while (!isdigit(ch) && ch != '-') ch = getchar(); 
    if (ch == '-') w = -1, ch = getchar(); 
    while (isdigit(ch)) data = 10 * data + ch - '0', ch = getchar(); 
    return w * data; 
} 
const int INF = 2e9; 
const int MAX_N = 1e6 + 5; 
typedef vector<int> :: iterator iter; 
vector<int> in[MAX_N], ot[MAX_N]; 
struct Graph { int to, cost, next; } e[MAX_N << 1]; 
int fir[MAX_N], e_cnt; 
void clearGraph() { memset(fir, -1, sizeof(fir)); e_cnt = 0; } 
void Add_Edge(int u, int v, int w) { e[e_cnt] = (Graph){v, w, fir[u]}, fir[u] = e_cnt++; } 
int pa[16][MAX_N], dep[MAX_N], dfn[MAX_N], tim; 
void dfs(int x, int fa) { 
	dfn[x] = ++tim; 
	if (fa) dep[x] = dep[fa] + 1; 
	pa[0][x] = fa; 
	for (int i = 1; i < 16; i++) 
		pa[i][x] = pa[i - 1][pa[i - 1][x]]; 
	for (int i = fir[x]; ~i; i = e[i].next) dfs(e[i].to, x); 
} 
int LCA(int x, int y) { 
	if (dep[x] < dep[y]) swap(x, y); 
	for (int i = 15; ~i; i--) 
		if (dep[pa[i][x]] >= dep[y]) x = pa[i][x]; 
	if (x == y) return x; 
	for (int i = 15; ~i; i--) 
		if (pa[i][x] != pa[i][y]) x = pa[i][x], y = pa[i][y]; 
	return pa[0][x]; 
} 
int N, M, K, tot, v[MAX_N], d[MAX_N]; 
int t[MAX_N], cnt; 
int sl[MAX_N], sr[MAX_N], pl[MAX_N], pr[MAX_N]; 
bool cmp(const int &i, const int &j) { return dfn[d[abs(i)]] < dfn[d[abs(j)]]; } 
void build(int x) { 
	cnt = 0; 
	for (iter i = in[x].begin(); i != in[x].end(); ++i) t[++cnt] = *i; 
	for (iter i = ot[x].begin(); i != ot[x].end(); ++i) t[++cnt] = -*i; 
	sort(&t[1], &t[cnt + 1], cmp); 
	for (int i = 1; i <= cnt; i++) { 
		pl[i] = ++tot, pr[i] = ++tot; 
		sl[i] = ++tot, sr[i] = ++tot; 
		if (i > 1) {
			Add_Edge(pl[i - 1], pl[i], 0), Add_Edge(pr[i - 1], pr[i], 0); 
			Add_Edge(sl[i], sl[i - 1], 0), Add_Edge(sr[i], sr[i - 1], 0); 
		} 
		if (t[i] > 0) Add_Edge(t[i], pl[i], 0), Add_Edge(t[i], sl[i], 0); 
		else t[i] = -t[i], Add_Edge(pr[i], t[i], 0), Add_Edge(sr[i], t[i], 0); 
	} 
	for (int i = 1; i < cnt; i++) { 
		int w = dep[LCA(d[t[i]], d[t[i + 1]])]; 
		Add_Edge(pl[i], pr[i + 1], w), Add_Edge(sl[i + 1], sr[i], w); 
	} 
} 
priority_queue<pair<int, int>, vector<pair<int, int> >, greater<pair<int, int> > > que; 
bool vis[MAX_N]; 
int dis[MAX_N]; 
void dijkstra() { 
	while (!que.empty()) { 
		pair<int, int> p = que.top(); que.pop(); 
		int x = p.second; 
		if (dis[x] < p.first) continue; 
		for (int i = fir[x]; ~i; i = e[i].next) { 
			int v = e[i].to, w = e[i].cost + ::v[v];
			if (!vis[v] && dis[x] + w < dis[v]) { 
				dis[v] = dis[x] + w; 
				que.push(make_pair(dis[v], v)); 
			} 
		} 
	} 
} 
int main () { 
#ifndef ONLINE_JUDGE 
    freopen("cpp.in", "r", stdin);
	freopen("cpp.out", "w", stdout);
#endif
	int T = gi(); 
	while (T--) { 
		clearGraph(); 
		for (int i = 0; i <= 1e6; i++) v[i] = d[i] = 0, dis[i] = INF, in[i].clear(), ot[i].clear(); 
		N = gi(), M = tot = gi(), K = gi(); 
		for (int i = 1; i <= M; i++) { 
			int x = gi(), y = gi(); v[i] = gi(), d[i] = gi(); 
			if (x == 1) que.push(make_pair(dis[i] = v[i], i)); 
			in[y].push_back(i), ot[x].push_back(i); 
		} 
		for (int i = 1; i < K; i++) { 
			int x = gi(), y = gi(); gi(); 
			Add_Edge(x, y, 0); 
		} 
		tim = 0, dfs(1, 0); 
		clearGraph(); 
		for (int i = 1; i <= N; i++) build(i); 
		dijkstra(); 
		for (int i = 2; i <= N; i++) { 
			int ans = INF; 
			for (iter j = in[i].begin(); j != in[i].end(); ++j) ans = min(ans, dis[*j]); 
			printf("%d
", ans); 
		} 
	} 
    return 0; 
}